It’s been over a century since Einstein firs proposed his Theory of General Relativity, his groundbreaking proposal for how gravity worked on large scales throughout the cosmos. And yet, after all that time, experiments are still being conducted that show that Einstein’s field equations were right on the money. And in some cases, old experiments are finding new uses, helping astronomers to unlock other astronomical mysteries.
Case in point: using the Hubble Space Telescope, NASA astronomers have repeated a century-old test of General Relativity to determine the mass of a white dwarf star. In the past, this test was used to determine how it deflects light from a background star. In this case, it was used to provide new insights into theories about the structure and composition of the burned-out remnants of a star.
White dwarfs are what become of a star after it has exited the Main Sequence of its lifespan after exhausting their nuclear fuel. This is followed by the star expelling most of its outer material, usually through a massive explosion (aka. a supernova). What is left behind is a small and extreme dense (second only to a neutron star) which exerts an incredible gravitational force.
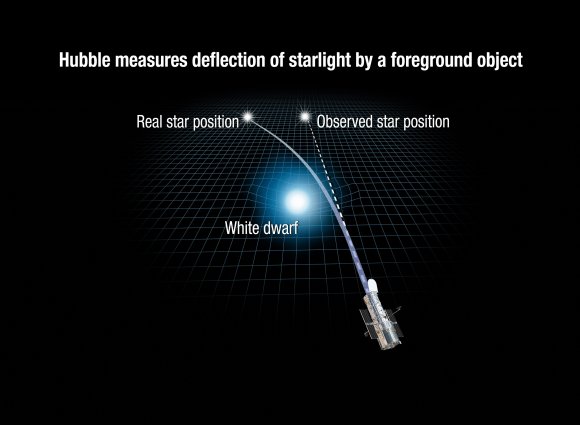
This attribute is what makes white dwarfs a good means for testing General Relativity. By measuring how much they deflect the light from a background star, astronomers are able to see the effect gravity has on the curvature of spacetime. This is precisely similar to what British astronomer Sir Arthur Eddington did in 1919, when he led an expedition to determine how much the Sun’s gravity deflected the light of a background star during a solar eclipse.
Known as gravitational microlensing, this same experiment was repeated by the NASA team. Using the Hubble Space Telescope, they observed Stein 2051B – a white dwarf located just 17 light-years from Earth – on seven different occasions during a two-year period. During this period, it passed in front of a background star located about 5000 light-years distant, which produced a visible deviation in the path of the star’s light.
The resulting deviation was incredibly small – only 2 milliarseconds from its actual position – and was only discernible thanks to the optical resolution of Hubble’s Wide Field Camera 3 (WFC3). Such a deviation would have been impossible to detect using instruments that predate Hubble. And more importantly, the results were consistent with what Einstein predicted a century ago.
As Kailash Sahu, an astronomer at the Space Telescope Science Institute (STScI) and the lead researcher on the project, explained in a NASA press release, this method is also an effective way to test a star’s mass. “This microlensing method is a very independent and direct way to determine the mass of a star,” he said. “It’s like placing the star on a scale: the deflection is analogous to the movement of the needle on the scale.”

The deflection measurement yielded highly-accurate results concerning the mass of the white dwarf star – roughly 68 percent of the Sun’s mass (aka. 0.68 Solar masses) – which was also consistent with theoretical predictions. This is highly significant, in that it opens the door to a new and interesting method for determining the mass of distant stars that do not have companions.
In the past, astronomers have typically determined the mass of stars by observing binary pairs and calculating their orbital motions. Much in the same way that radial velocity measurements are used by astronomers to determine if a planet has a system of exoplanets, measuring the influence two stars have on each other is used to determine how much mass each possesses.
This was how astronomers determined the mass of the Sirius star system, which is located about 8.6 light years from Earth. This binary star system consists of a white supergiant (Sirius A) and a white dwarf companion (Sirius B) which orbit each other with a radial velocity of 5.5 km/s. These measurements helped astronomers determine that Sirius A has a mass of about 2.02 Solar masses while Sirius B weighs in at 0.978 Solar masses.
And while Stein 2051B has a companion (a bright red dwarf), astronomers cannot accurately measure its mass because the stars are too far apart – at least 8 billion km (5 billion mi). Hence, this method could be used in the future wherever companion stars are unavailable or too distant. The Hubble observations also helped the team to independently verify the theory that a white dwarf’s radius can be determined by its mass.

This theory was first proposed by Subrahmanyan Chandrasekhar in 1935, the Indian-American astronomer whose theoretical work on the evolution of stars (and black holes) earned him the Nobel Prize for Physics in 1983. They could also help astronomers to learn more about the internal composition of white dwarfs. But even with an instrument as sophisticated as the WFC3, obtaining these measurements was not without its share of difficulties.
As Jay Anderson, an astronomer with the STScI who led the analysis to precisely measure the positions of stars in the Hubble images, explained:
“Stein 2051B appears 400 times brighter than the distant background star. So measuring the extremely small deflection is like trying to see a firefly move next to a light bulb. The movement of the insect is very small, and the glow of the light bulb makes it difficult to see the insect moving.”
Dr. Sahu presented his team’s findings yesterday (June 7th) at the American Astronomical Society meeting in Austin, Texas. The team’s result will also appear in the journal Science on June 9th. And in the future, the researchers plan to use Hubble to conduct a similar microlensing study on Proxima Centauri, our solar system’s closest stellar neighbor and home to the closest exoplanet to Earth (Proxima b).
It is important to note that this is by no means the only modern experiment that has validated Einstein’s theories. In recent years, General Relativity has been confirmed through observations of rapidly spinning pulsars, 3D simulations of cosmic evolution, and (most importantly) the discovery of gravitational waves. Even in death, Einstein is still making valued contributions to astrophysics!
Further Reading: NASA


If this measurement could be done for a black hole, I wonder if it could shed light whether the black hole’s mass is concentrated at a singularity in the center versus the spherical shell of the event horizon? I think the bending of light would be slightly different for the two cases. However, perhaps the much more complex curvature of spacetime near a spinning black hole cannot yet be sufficiently modeled.
Using that language, ” Einstein is right or wrong” still bugs me. Of course Einstein was right about general relativity. The only question that remains is whether general relativity has limits. To prove that you need an observation that does not fit the model, so to speak. Inaccuracies in Mercury’s orbit exposed Newton’s law of gravitation to be limited and Einstein formulated general relativity to resolve the problem. So far ever more precise measurements have not found flaws in general relativity but we keep looking, as we should. Finding a flaw would uncover new physics and be considered a major breakthrough in science.
This observation is not about ‘proving’ GR. You want to observe light deviation by a known mass to do that, which is what Eddington did a century ago. This observation is about using GR to calculate an unknown mass. Can’t have it both ways.
Also, “usually through a massive explosion (aka. a supernova)”: No. White dwarfs are the remnant of smaller mass stars (up to a few solar masses) which don’t go SN.
Ya, screw proof! Just keep believing, brah! I believe in you!