Unless Einstein is wrong, a black hole is defined by three properties: mass, spin, and electric charge. The charge of a black hole should be nearly zero since the matter captured by a black hole is electrically neutral. The mass of a black hole determines the size of its event horizon, and can be measured in several ways, from the brightness of the material around it to the orbital motion of nearby stars. The spin of a black hole is much more difficult to study.
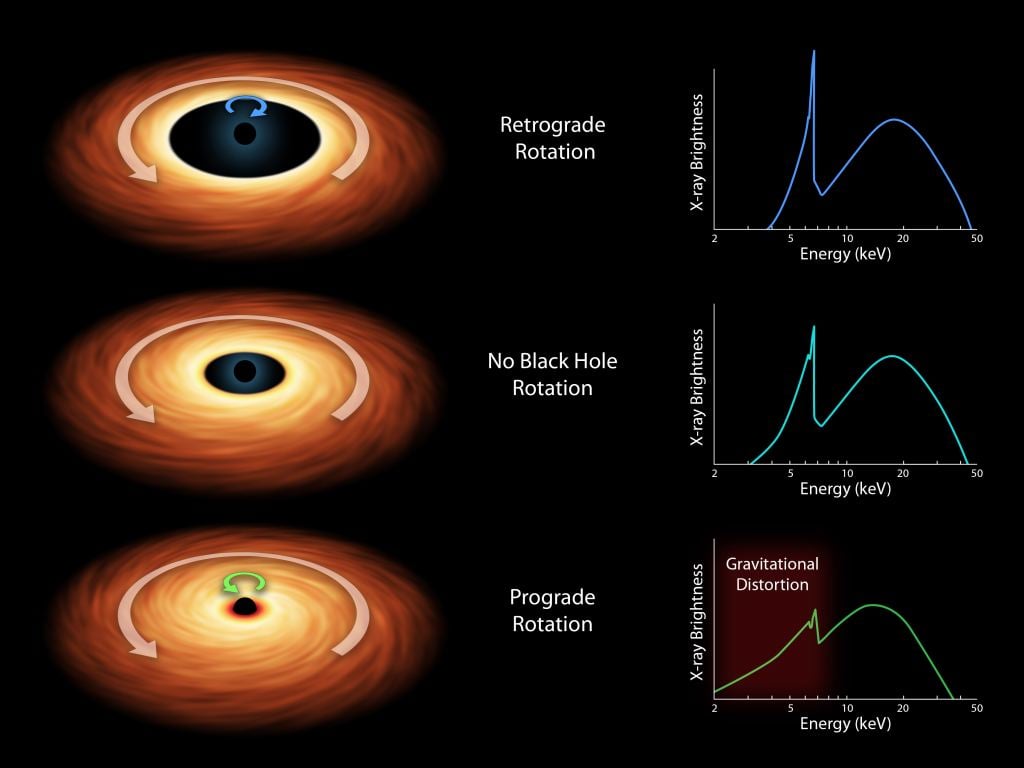
A black hole's spin is basically its rotation. Just as stars and planets rotate on their axis, so do black holes. The difference is that black holes don't have a physical surface like stars and planets. Black hole spin, like mass, is a spacetime property. Spin determines how space is warped around a black hole. To measure the spin of a black hole, you need to study how matter behaves near it.
The spin of some supermassive black holes has been measured. With a few active black holes, we can study the x-rays emitted by their accretion disks. X-ray light from the disk is given a boost of energy from the rotation, and by measuring that boost, we can determine the spin. Another way is to take a direct image of the black hole, as we did with the one at the center of M87. The ring of light we see is brighter on the side rotating toward us.
But we don't know the spin of the closest supermassive black hole, the one in our own galaxy. Our black hole isn't very active, and it's much smaller than the one in M87. We can't measure its spin by observing light near it. But a new paper in *Astrophysical Journal Letters* argues that there is another way to measure spin.
Their method uses a property known as frame dragging. When a mass rotates, it twists space around it slightly. We know it is real because we've measured the frame-dragging effect of Earth's rotation. The spin of a black hole creates the same kind of frame-dragging, and by measuring it, we can determine the black hole's spin. We can't put a probe in orbit around the black hole the way we did with Earth, but we can use the next best thing.
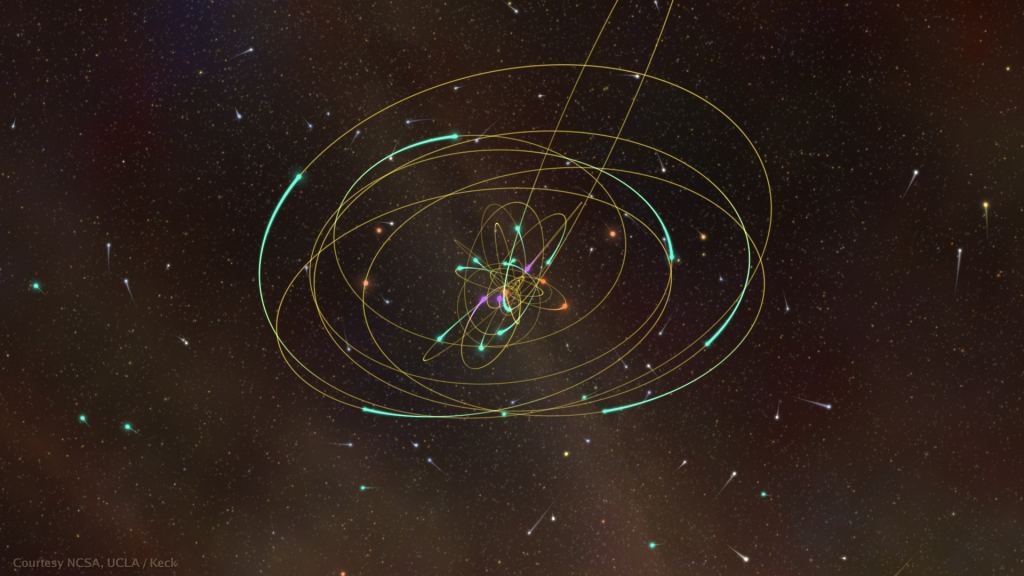
Hundreds of stars orbit the black hole at the center of our galaxy. About forty of them, known as S-stars, have orbits with a close approach to the black hole. Over time their orbits are shifted by the frame-dragging effect. If we can measure these shifts, we can measure the spin—the greater the spin, the greater the orbit shift.
In this new work, the team studied the orbits of the S-stars and found no frame dragging shift. Given how well we know the orbits of these stars, we know the black hole at the center of our galaxy must be rotating slowly. The team determined that its spin can be no more than 0.1 on a scale from 0 to 1, meaning it is rotating less than 10% of the maximum possible spin for a black hole. By contrast, the spin of M87's black hole is at least 0.4.
Reference: Fragione, Giacomo, and Abraham Loeb. " An Upper Limit on the Spin of SgrA* Based on Stellar Orbits in Its Vicinity." *The Astrophysical Journal Letters* 901.2 (2020): L32.
Reference: Nemmen, Rodrigo. " The Spin of M87*." *The Astrophysical Journal Letters* 880.2 (2019): L26.
 Universe Today
Universe Today