[/caption]
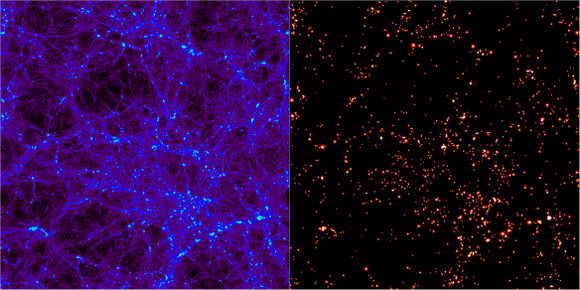
One of the successes of the ΛCDM model of the universe is the ability for models to create structures of with scales and distributions similar to those we view in the universe today. Or, at least that’s what astronomers tell us. While computer simulations can recreate numerical universes in a box, interpreting these mathematical approximations is a challenge in and of itself. To identify the components of the simulated space, astronomers have had to develop tools to search for structure. The results has been nearly 30 independent computer programs since 1974. Each promises to reveal the forming structure in the universe by finding regions in which dark matter halos form. To test these algorithms out, a conference was arranged in Madrid, Spain during the May of 2010 entitled “Haloes going MAD” in which 18 of these codes were put to the test to see how well they stacked up.
Numerical simulations for universes, like the famous Millennium Simulation begin with nothing more than “particles”. While these were undoubtedly small on a cosmological scale, such particles represent blobs of dark matter with millions or billions solar masses. As time is run forwards, they are allowed to interact with one another following rules that coincident with our best understanding of physics and the nature of such matter. This leads to an evolving universe from which astronomers must use the complicated codes to locate the conglomerations of dark matter inside which galaxies would form.
One of the main methods such programs use is to search for small overdensities and then grow a spherical shell around it until the density falls off to a negligible factor. Most will then prune the particles within the volume that are not gravitationally bound to make sure that the detection mechanism didn’t just seize on a brief, transient clustering that will fall apart in time. Other techniques involve searching other phase spaces for particles with similar velocities all nearby (a sign that they have become bound).
To compare how each of the algorithms fared, they were put through two tests. The first, involved a series of intentionally created dark matter halos with embedded sub-halos. Since the particle distribution was intentionally placed, the output from the programs should correctly find the center and size of the halos. The second test was a full fledged universe simulation. In this, the actual distribution wouldn’t be known, but the sheer size would allow different programs to be compared on the same data set to see how similarly they interpreted a common source.
In both tests, all the finders generally performed well. In the first test, there were some discrepancies based on how different programs defined the location of the halos. Some defined it as the peak in density, while others defined it as a center of mass. When searching for sub-halos, ones that used the phase space approach seemed to be able to more reliably detect smaller formations, yet did not always detect which particles in the clump were actually bound. For the full simulation, all algorithms agreed exceptionally well. Due to the nature of the simulation, small scales weren’t well represented so the understanding of how each detect these structures was limited.
The combination of these tests did not favor one particular algorithm or method over any other. It revealed that each generally functions well with regard to one another. The ability for so many independent codes, with independent methods means that the findings are extremely robust. The knowledge they pass on about how our understanding of the universe evolves allows astronomers to make fundamental comparisons to the observable universe in order to test the such models and theories.
The results of this test have been compiled into a paper that is slated for publication in an upcoming issue of the Monthly Notices of the Royal Astronomical Society.

On page 9 the article does discuss smoothed particle hydrodynamics. This approach has always struck me as preferable to many body codes in modeling DM. It seems preferable it the many body part of the algorithm works the dynamics of clusters of matter that form galaxies.
LC
Nice article, broadens one’s view!
Spontaneously I’m not sure why you would prefer one algorithm over another unless you can measure the difference. FWIW, I was recently reminded that continuous models may have advantage over discrete in computing time (which I gather wasn’t used for some sort of “ROI evaluation” here):
“This creates 3^D=3 billion bins (for D=20). Even if one had a huge simulation with a billion Higgs boson decays, the bins would never contain a meaningful number of events with which to compute an average bias (e.g. true Higgs mass minus measured mass).
There was a way out. One needed to stop thinking in terms of a discrete matrix (as was the typical approach), but in terms of continuous variables. I wrote an algorithm that did precisely that: if you had a real data event with a measured mass M and with a certain value of the 20 variables, you could move around in the neighborhood of the point in the 20-dimensional space corresponding to the data event, and ask to each Monte Carlo event lying nearby in the space whether the reconstructed mass one could compute with it was over- or undermeasured. If one asked enough events for a meaningful average, that would be enough!
So one needed to “inflate” a hyperball in the multi-dimensional space, capturing Monte Carlo events that were “close enough” to the data event to be corrected.”
Different case of discreteness obviously, but neatly (IMO) showing how “out of the box” solutions may surrender a solution for computing power problems.
This may be out of place here but, it was recently suggested, by HSBC I believe, that the “Recent Comment” list be increased; I second that. Seems the articles are coming at a faster clip and it’s getting harder to keep up with the discussions. Thanks UT, I enjoy this site and appreciate all the hard work you all do to make it possible.
I’d like to “third” that suggestion wjwbudro. 🙂
It would definitely help out keeping track of all the newer posts, especially on loooong threads and comment threads that span more than one page. And definitely keep up the good work, your efforts are greatly appreciated.
DM appears best modeled as a Navier-Stokes type of fluid. The galactic luminous stuff might be modeled as particles, say one particle = one unit of M33 mass =~ .10 Milky Way mass. The smoothed hydro-code could place the particles on an Eulerian frame in the hydro-flow.
LC
@LBC
Turbulence and other time dependent chaotic behaviors seen in these many fluid flows will be the basis for what passes as density varations due to the inertia of this fluid “matter’. Since this is DM we need not worry about convective acceleration as DM interacts weakly, if at all, with those forces known to us (so far) and all this means that this solution is a clever way of viewing the 4D boundary conditions of these interacting DM to DM flows.
Just think of it, we can have Mark Time after all (another Firesign Theatre reference of course).The eddies, currents, “sand bars”, tiki bars, but wait, that is a different thread, sorry, I’ll leave now.
Mike C
The turbulence probably has some limiting scale. I like to think of galaxies in DM as like dust cobwebs, in an attic room filled with cobwebs, and where sunlight coming through causes them to glint. The thing is that the room is expanding, or the walls are moving out. In the last 3 to 4 billion years these wall have started to exponentially move outwards. So this probably puts some scale limit on turbulence.
The structure of these filaments, walls and voids must have some Hausdorff dimension or fractal characterization. When the Planck probe is done and the data is downloaded I might take the SDDSS data on this and run digital convolutions of the two data sets to see what happens.
LC
i thought the ‘dark’ nomenclature was only applied to tentative hypotheses and concepts about which little is known? since we’re now so confident of the existence of dark matter and know so much about it’s role in the evolution of galaxies and what not… shouldn’t it be given a name that is less… mysterious?
Well, we know that it exists and that it mostly/only interacts with ordinary matter by gravity. But that’s more or less all. Anything else is, say, reasonable speculation. I think, it’s still mysterious enough to be called dark matter (and, btw, the name is accurate: This matter is truly dark).
DM is called dark because it does not interact by the electromagnetic radiation. As such light or IR radio waves etc do not reflect off of DM, nor are they absorbed and emitted by DM. Hence this is the origin of the term dark. What is mysterious also is that we do not know where DM sits in the symmetry schemes of elementary particles. Theory pretty strongly suggests DM is some aspect of supersymmetry, where DM consists of the superpartners of the neutrino, Higgs field, photon and Z particle in a condensate state.
We do know that DM exists because of its gravitational interaction with light. The Einstein lensing due to DM can’t be accounted for by ordinary matter.
LC
wow, really good answers, thanks guys! mysterious indeed!
A Navier-Stokes type of fluid nevertheless interacts with ordinary matter by gravity. Hausdorff dimension or fractal characterization would depend on convective acceleration, resulting in different cases of discreteness. Therefore most of the algorithms would work out the dynamics of clusters of matter that form galaxies.
That should be the case, and the ordinary matter would flow on the Eulerian frame of the DM “fluid” flow.” I will confess I am not that experienced in this stuff, but this would be how I would approach something of this nature.
LC