[/caption]
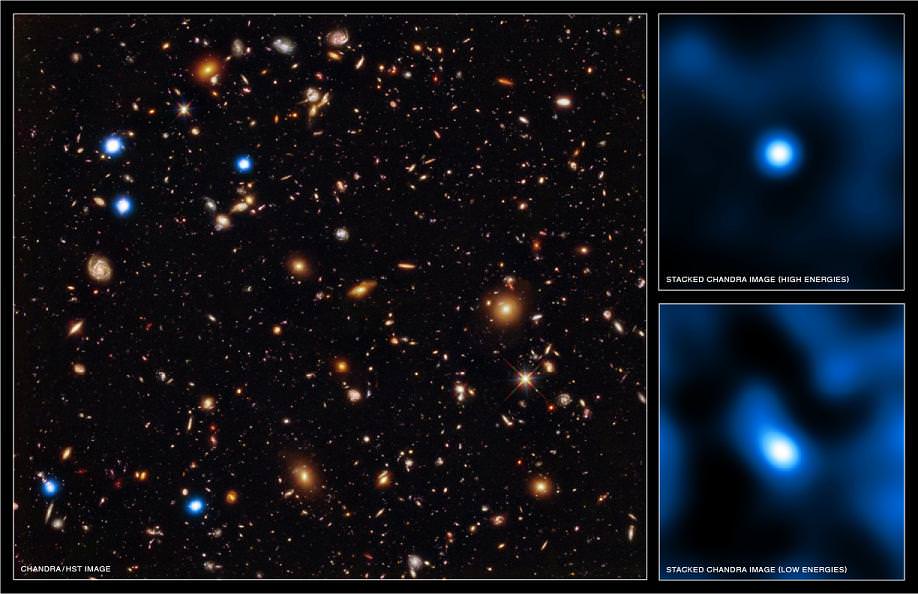
For more than six weeks, the watchful eye of NASA’s Chandra X-ray Observatory kept track of a small portion of sky dubbed the Chandra Deep Field South (CDFS). Its object was to research 200 distant galaxies dating back to about 800 million to 950 million years old. What Chandra was looking for was evidence of massive black holes. The deepest evidence yet…
When combined with very deep optical and infrared images from NASA’s Hubble Space Telescope, the new Chandra data leads astronomers to speculate that young black holes may have evolved in unison with their young galaxies. “Until now, we had no idea what the black holes in these early galaxies were doing, or if they even existed,” said Ezequiel Treister of the University of Hawaii, lead author of the study appearing in the June 16 issue of the journal Nature. “Now we know they are there, and they are growing like gangbusters.”
What does this new information mean? The massive growth of the black holes in the CDFS are just shy of being a quasar – the super-luminous by-product of material slipping over the event horizon. “However, the sources in the CDFS are about a hundred times fainter and the black holes are about a thousand times less massive than the ones in quasars.” How often did it occur in the new data? Try between 30 and 100% of the case studies, resulting in a estimated 30 million supermassive black holes in the early Universe.
“It appears we’ve found a whole new population of baby black holes,” said co-author Kevin Schawinski of Yale University. “We think these babies will grow by a factor of about a hundred or a thousand, eventually becoming like the giant black holes we see today almost 13 billion years later.”
While the existence of these early black holes had been predicted, no observation had been made until now. Due to their natural “cloaking devices” of gas and dust, optical observation had been prohibited, but x-ray signatures don’t lie. The concept of tandem black hole / galaxy growth has been studied closer to home, but taking a look further back into time and space has revealed growth a hundred times more than estimated. These new Chandra results are teaching us that this connection begins at the beginning.
“Most astronomers think in the present-day universe, black holes and galaxies are somehow symbiotic in how they grow,” said Priya Natarajan, a co-author from Yale University. “We have shown that this codependent relationship has existed from very early times.”
Theories also abound which imply neophyte black holes may have played “an important role in clearing away the cosmic “fog” of neutral, or uncharged, hydrogen that pervaded the early universe when temperatures cooled down after the Big Bang”. But to the contrary, the new Chandra findings point towards the pervasive materials stopping ultraviolet radiation before the re-ionization process can occur. Resultant stars and dormant black holes are the most likely culprit to have cleared space for the cosmic dawn.
Although the Chandra X-ray Observatory is up to the task of picking up on uber-faint objects at incredible distances, these baby black holes are so veiled that only a few photons can slip through, making individual detection impossible. To gather this new data, the team employed Chandra’s directional abilities and tallied the hits near the positions of distant galaxies and found a statistically significant signal.
Original Story Source: Chandra News.

An interesting question to ponder is whether these black holes were generated in the inflationary or pre-inflationary period. Inflation removed inhomogeneities and it is unlikely black hole collapse occurred much once inflation got going.
LC
With all due respect I question the statement “30 million” of anything quantified to a universe of a “billion” years based upon the proposition that nobody really knows how old the universe is, and how much of anything is in it.
“Simplicity….source of all truth.”
We have a pretty good idea how old the universe is. We also pretty well know the distribution of mass-energy in it.
LC
What is this great Truth™ that you refer to, oh wise one(!), as if I didn’t know already?
Are Population III stars a viable candidate? Or, for that matter, direct growth?
“Go to Singularity, do not pass ignition, do not collect $100”
The funny thing is it is hard to grow a moderate sized black hole. To get a particle into a black hole from a distance you have to aim pretty much dead on. Otherwise the particle goes into an orbit around the black hole. With bulk material as it enters the region of intense gravity it heats up and the pressure tends to throw much of it out before it crosses the horizon. So a 10 to 100 solar mass black hole will grow, but at a moderate pace.
A PopIII star supernovae or similar explosion might generate black holes. I am not sure of the astrophysics of these, but a core implosion should give a black hole. But it would then grow rather slowly. So there is a question on how a 30 million solar mass black hole got formed that quickly.
It could be that black holes emerged in the most early universe, where these are some local inhomogeneous distributions that inflation could not flatten out. This does pose some problems with the entropy of the early universe though. However, assuming this happened the density of matter in this early universe might have provided the engorgement of the black hole to swell it up to enormous sizes in the first few minutes into the big bang.
LC
There was an article here on UT about BH growth being speed up when the BH rotates in the opposite direction of infalling matter. That would make alot of sense, and it would be relatively common as random protogalaxy-mergers could funnel matter towards the centre at any angle. Co-rotating BH would then grow much slower than counter-rotating ones.
That still would require a seed, and higher mass-end popIII stars looks like excellent candidates from a theoretical viewpoint. I hope we will get answers soon with new telescopes in the making.
It is the case that matter falling in with an angular momentum oppositely directed from that of the black hole will preferentially fall in. The entropy dS = dM – Jd? , for M the mass, and J the angular momentum and ? the “action-angle” is increased more if the black hole is “spun down.” So a black hole with a counter rotating accretion disk will absorb matter at a faster rate.
The generation of black holes in the earliest universe does pose entropy problems. It would be best if the early universe did not generate a whole lot of them. People who work out the astrophysical phenomenology of black hole growth do have a bit of a task ahead of them. I think this is a bit of an open question at this time.
LC
If BHs did form very early, presumably they would do so more frequently in denser regions thus reducing the local density of the remaining plasma. Could that have contributed significantly to the uniformity of the CMBR?
Does the idea of direct growth have any merit – my limited understanding is that the larger the mass of the black hole, the lower the density required to cause collapse. I’m thinking of the scenario where you have some nascent stellar core in a cluster that grows big enough fast enough that rather than igniting, it simply becomes overwhelmed by it’s own gravity and collapses.
(I seem to recall reading somewhere onceupon a time that a sphere of water 1 light year across would be massive enough that its Schwarzchild Radius would exceed its physical radius, causing it to collapse into a singularity).
The radius of a black hole horizon scales directly with its mass R = 2GM/c^3. This is different than how an ordinary body increases its size. Given the accumulation of matter with a constant density the radius grows as the cube root of the mass.
LC
Which means that, if I’ve done my substitutions correctly (not a given at 7am) then we wind up with:
m=[(3*c^5)/(32*Pi*Rho*G^3)]^0.5
For satisfying the condition r_s = r
I guess I am trying to figure out what you did here. There are elements of the spacetime metric, a sort of Pythagorean Theorem distance that is infinitesimally small
ds^2 = Adt^2 – A^{-1}dr^2 – r^2d?^2
for A = 1 – 2GM/rc^2. Where this comes from requires a deeper knowledge of general relativity. The factor A = 0 at r = 2GM/c^2, which is where the event horizon is. So the mass and radius of the black hole scale proportionally r = constant x M. This is different from a body where mass scales with volume M = ?V = 4??r^3/3 for ? = density a constant.
LC
Starting with:
1. ?=m/v
2. v=(4*?*r^3)/3
3. R = 2GM/c^2
Rearrange 1 ro solve for v
1a. v=m/?
Substitute 1a into 2
2a. m/?=(4*?*r^3)/3
Solve 2a, for r:
2b. r=[(3*m)/(4*?*?]^(1/3)
Substitute 2b into 3, because the condition we’re interested in is R=r.
3a. 2GM/c^2 = [(3*m)/(4*?*?]^(1/3)
And finally, assuming that M in 3. isn’t normalized into solar masses, or some such, rearrange 3a. to solve for m, for which I arrive at:
m=[(3*c^5)/(32*?*?*G^3)]^0.5
To derive the mass at which, assuming a uniform density, the schwarzchild radius of the object exceeds its physical radius.
That is – assuming my skills are up to par, which isn’t neccessarily a given at 7am.
This is getting crowded! A black hole is not a solid body, so while your calculation is formally correct it does not pertain to the problem of black holes. Matter that falls below the event horizon enters a region where curvature diverges in its future. The singularity is a future spacelike region where curvatures diverge.
Your formula has some relevance for the amount of mass of a certain density is close to imploding into a black hole.
LC
Which is what I was trying to calculate. 🙂
Yo Tammy, at the penultimate paragraph, in the last sentence, “culprit” should plural as is the context of that sentence.
Also, referring to the last paragraph, I realize that you re-worded the original press release so as to not plagiarize it, but the original term “find” in the last sentence now sounds awkward, so I would suggest substituting it with the past tense and past participle term “found”.
Um… I’ll get my coat and see myself out…
*Starts-up truck*… *Drives off*…