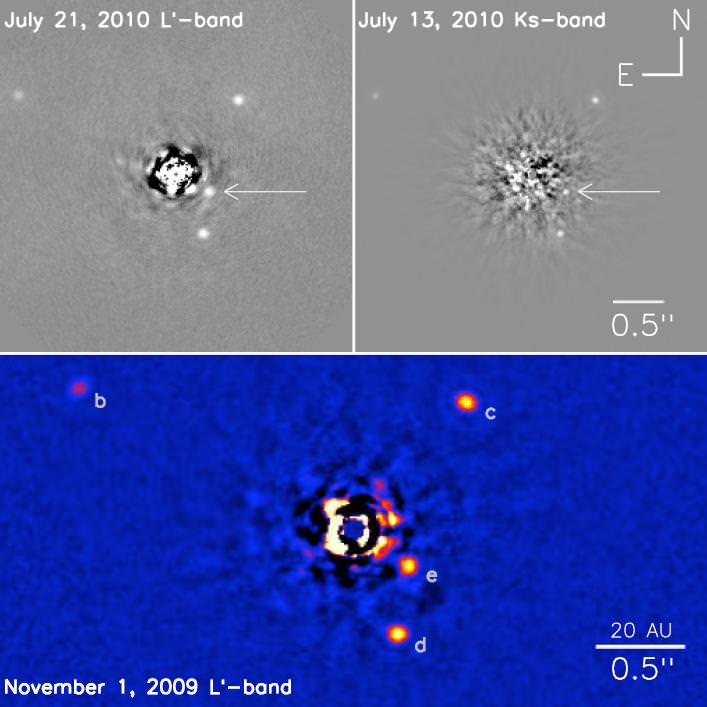
[/caption]
Late last year, astronomers using the Keck II telescope released the first direct image of a planetary system including four planets. These planets orbited the star HR 8799 and were taken in the J and L bandpasses which are in the near-infrared portion of the spectrum. Since then the team has collected new data using the same telescope, extending the spectral range into the mid-infrared portion of the spectra.
The new images are important to astronomers because this provides a more complete understanding of the distribution of radiation that the planets are emitting. This can be compared to models of planetary formation, allowing these young planets to act as a test bed. Previous comparison to models have suggested that these planets have cool, dusty atmospheres without the presence of methane or other common absorbing molecules.
The team hopes that the new observations will help distinguish between the various models that explain this deficiency of methane. Unfortunately, getting good observations in this portion of the spectra is challenging. In particular, at the Keck telescope, the design of the telescope itself makes observations especially challenging due to portions of the instrument themselves emitting in the infrared, masking the faint signals from the planet.
To bring out the planets, the team developed a new technique to help clean the images of the unwanted noise. They estimate that their new technique is nine times more efficient than previously used techniques. To do this, they moved the telescope slightly between images, allowing the patterns of interference to change between exposures, thereby making them more apparent and easier to remove.
When the results were analyzed and compared to models, the team found that they were in good agreement with predictions of planetary evolution for planets c and d. However, for planet b, the models predicted a planet with a radius that would be too small to account for the observed luminosity. The observations could be brought into agreement with the models by increasing the metallicity of the model.
With additional future observations, the team hopes to constrain these models and further investigate the atmospheres of these planets.
NOTE: I Emailed the authors of the paper to ask permission to reproduce the new image here, but have not gotten a reply. The one used above is the K and L band images from last year. To see the new ones, feel free to go to the paper directly.

Incredible.
Ferengi Rule of Acquisition #52: Never ask when you can take.
Kitteh Rulz Ov Pawz: No ask oen thar iz caek.
[LOLcat translation: Cat rule of thumb*: Don’t ask when there is cake.
*No numbers, cats don’t need math to take … um, decisions.]
Why did the planets not move in relationship to the 2009 image?
at 14.5 AU a 7x Jupiter mass planet would take about 45 years to go around a 1.5 solar mass star once .. the two images are only about six months apart, so that planet would have move only about 1% in its orbit between the two images .. which is probably not enough for the naked eye to notice … ps. the outer planet “b” would take about 450 years to go around its star
I’m not entirely sure. However, I think it may be due to the distance of these planets. Unlike many of the “hot jupiters” we’ve been finding, the innermost one yet discovered (e) is over 14 AU distant. Thus, it should orbit very slowly and not have a readily changing appearance.
This is illustrated by the change in positions between 2004 and 2008 in this image: http://www.universetoday.com/22173/time-magazine-top-10-scientific-discoveries-of-2008-space-and-physics-dominate/gemini1/
They most likely did, just not enough to be noticeable at the first glance, since they are more than or about 20 AU from the star and therefore have much longer years than 6 months between images.
Uranus, at about 20 AU, has orbital period at over 84 years.
http://en.wikipedia.org/wiki/Uranus
Largely Mana Brau has the right answer. The closest planet is 14.5 AU away, which put it at a Neptune orbital distance. The Kepler 3rd law gives that the square of the orbital frequency is proportional to the reciprocal of the cube of the orbital radius. So the orbital frequency is very small, or equivalently the period is very large. It is too large to measure any significant change in the angular position of the planet within an Earth-year period.
LC
Neptune is at about 30 AU ..
http://en.wikipedia.org/wiki/Neptune
I suppose I was thinking of Uranus. I suppose I lose marks on a 4th grade astronomy quiz.
If the star is 1.5 times a solar mass and Uranus is 20AU and this planet is at 14.5AU we can calculate the orbital period. We use Newton’s second law
m?^2r = GMm/r^2
and the angular frequency ? is
? = sqrt(GM/r^3)..
The orbital period is T = 2?/? = 2? sqrt{r^3/GM}. So we compute the ratio of Uranus’ period to the period of this T_u/T_e (e = e planet)
T_u/T_e = (r_u/r_e)^{3/2}*sqrt(M_hr/M__sol) = .586*.816 = .4784
T_u = 84 yr and so T_e = 40.2yr. So if in that period it rotates 360 degrees then in 6 months it would rotate 4.5 degrees.
I can’t attach pictures here, but one can actually see this! Play with the pictures on photoshop and draw a line through the star and planet in the the top left and bottom pictures. Compare the two lines and they are not the same! Now of course this presumes the orientations of the two photos are the same and so forth. However, there is a visual impact.
LC
test