Physics Archives

February 10, 2016February 11, 2016 by Markus Pössel

Gravitational Wave Detectors: How They Work

It’s official: this Thursday, February 11, at 10:30 EST, there will be parallel press conferences at the National Press Club in Washington, D.C., in Hannover, Germany, and near Pisa in Italy. Not officially confirmed, but highly probable, is that people running the LIGO gravitational wave detectors will announce the first direct detection of a gravitational wave. The first direct detection of minute distortions of spacetime, travelling at the speed of light, first postulated by Albert Einstein almost exactly 100 years ago. Nobel prize time.

Time to brush up on your gravitational wave basics, if you haven’t done so! In Gravitational waves and how they distort space, I had a look at what gravitational waves do. Now, on to the next step: How can we measure what they do? How do gravitational wave detectors such as LIGO work?

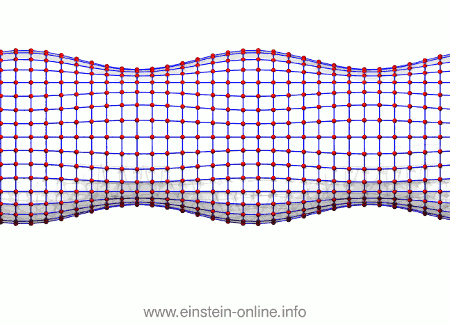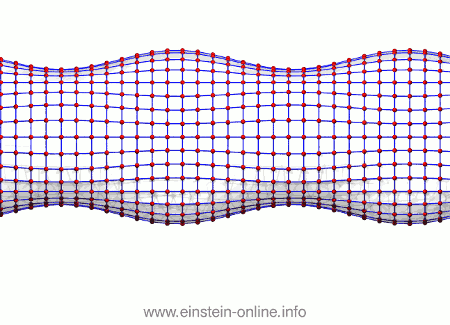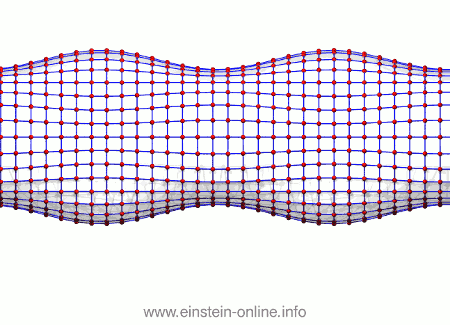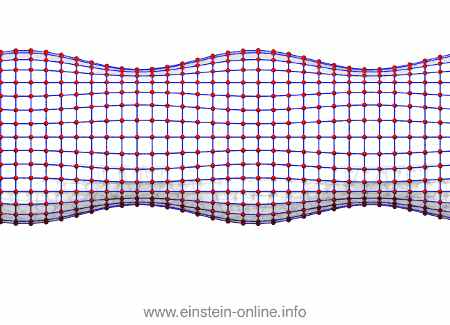
Recall that this is how a gravitational wave will change the distances between particles, floating freely in a circular formation in empty space: The wave is moving at right angles to the screen, towards you. I’ve greatly exaggerated the distance changes. For a realistic wave, even the giant distance between the Earth and the Sun would only change by a fraction of the diameter of a hydrogen atom. Tiny changes indeed.

How to detect something like this?

The first unsuccessful attempts to detect gravitational waves in the 1960s tried to measure how they make aluminum cylinders ring like a very soft bell. (Tragic story; Joe Weber [1919-2000], the pioneering physicist behind this, was sure he had detected gravitational waves in this way; after thorough analysis and replication attempts, community consensus emerged that he hadn’t.)

Afterwards, physicists came up with alternative scheme. Imagine that you are replacing the black point in the center of the previous animation with a detector, and the rightmost red particle with a laser light source. Now you send light pulses (represented here by fast red dots) from the light source to the detector; let’s first look at this with the gravitational wave switched off:

Every time a light pulse reaches the detector, an indicator light flashes yellow. The pulses are sent out regularly, they all travel at the same speed, hence they also reach the detector in regular intervals.

If a gravitational wave passes through this system, again from the back and coming towards you, distances will change. Let us keep our camera trained on the detector, so the detector remains where it is. The changing distance to the light source, and also the changing distances between the light pulses, and some of the changes in distance between light pulses and detector or source, are due to the gravitational wave. Here is what that would look like (again, hugely exaggerated):

Keep your eye on the blinking light, and you will see that its blinking is not so regular any more. Sometimes, the light blinks faster, sometimes slower. This is an effect of the gravitational wave. An effect by which we can hope to detect the gravitational wave.

“We” in this case are the radio astronomers working on what are known as Pulsar Timing Arrays. The sender of regular pulses are pulsars, rotating neutron stars sweeping a radio beam across our antennas like a cosmic lighthouse. The detectors are radio telescopes here on Earth. Detection is anything but easy. With a single pulsar, you’d need to track pulse arrival times with an accuracy of a few billionths of a second over half a year, and make sure you are not being fooled by various other sources of timing variations. So far, no gravitational waves have been detected in this way, although the radio astronomers are keeping at it.

To see how gravitational wave detectors like LIGO work, we need to make things a little more complex.

Interferometric gravitational wave detectors: the set-up

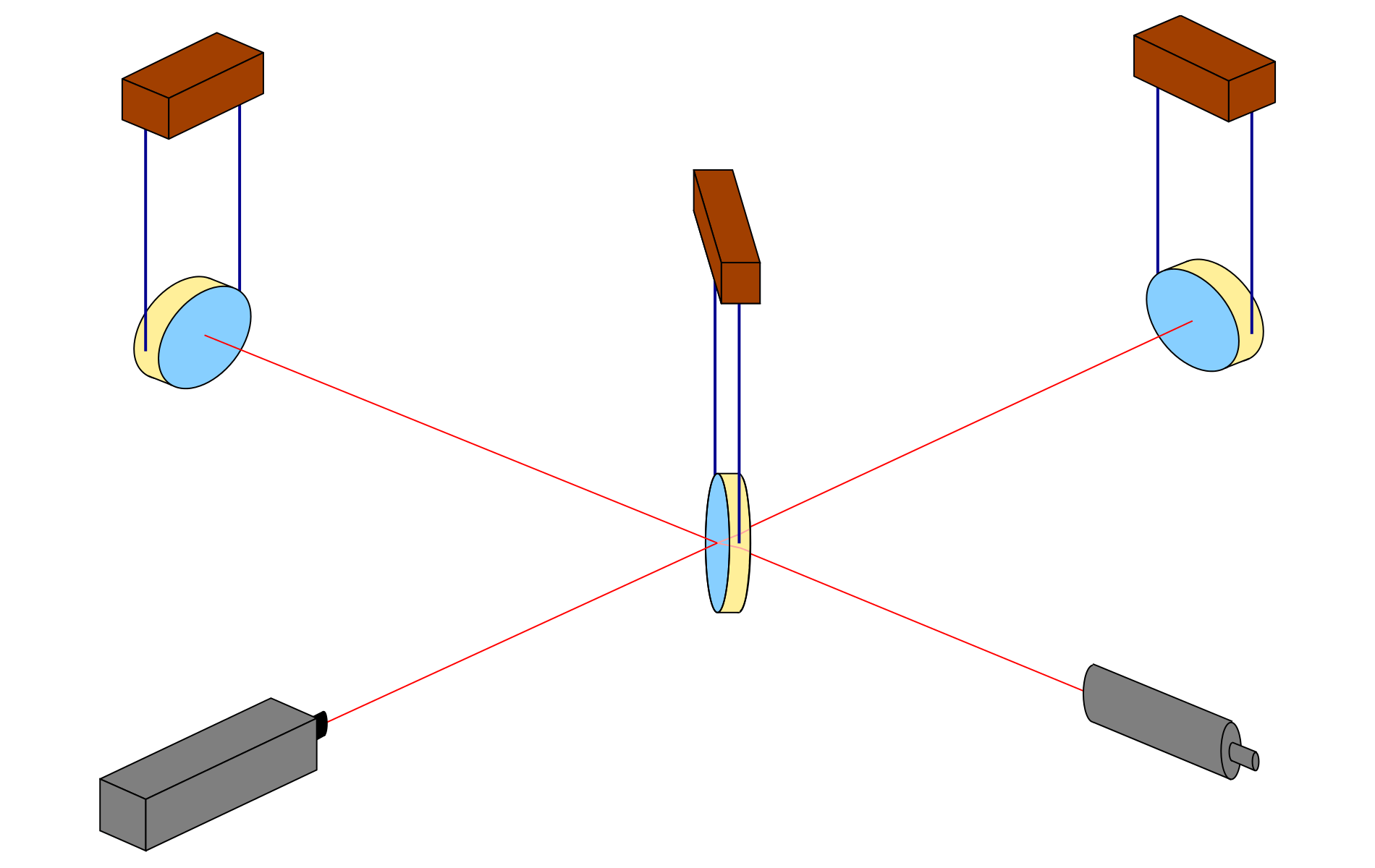
Here is the basic set-up: Two mirrors, a receiver (or “light detector”), a light source and what is known as a beamsplitter: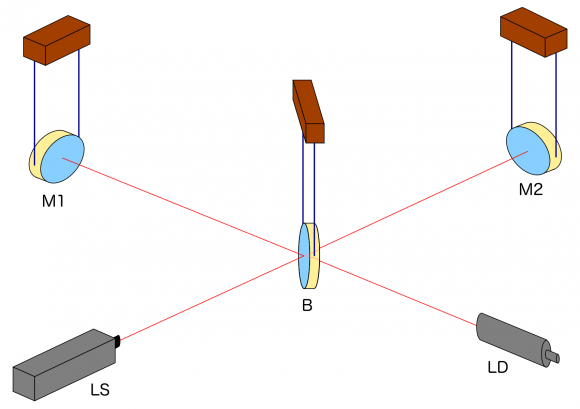

Light is sent into the detector from the (laser) light source LS to the beamsplitter B which, true to its name, sends half of the light on to the mirror M1 and lets the other half through to the mirror M2. At M1 and M2, respectively, the light is reflected back to the beam splitter. There, the light arriving from M1 (or M2) is split again, with half going towards the light detector LD, the other half back in the direction of the light source LS. We will ignore the latter half and pretend, for the sake of our simplified explanation, that all the light reaching B from M1 or M2 goes on to the light detector LD.

(To avoid confusion, I will always refer to LD as the “light detector” and take the unqualified word “detector” to mean the whole setup.)

This setup, by the way, is called a Michelson Interferometer. We’ll see below why it is a good setup for gravitational wave detectors.

In what follows, we will assume that the mirrors and the beam splitter, shown as being suspended, react to the gravitational wave in the same way freely floating particles would react. The key effects are between the mirrors and the beam splitter in what are called the two arms of the detector. Arm length is huge in today’s detectors, running to a few kilometers. In comparison, light source and light detector are very close to the beamsplitter; changes of the distances between these three do not signify.

Light pulses in a gravitational wave detector

Next, let us see how light pulses run through this detector. Here is the same setup, seen from above: 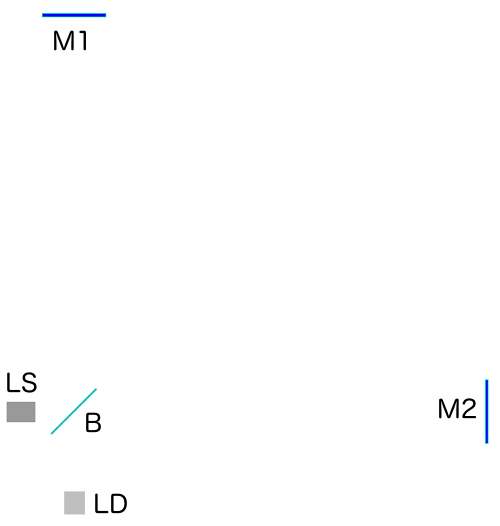Light source LS, the two mirrors M1 and M2, the beamsplitter B and the light detector LD: all present and accounted for.

Next, we let the light source emit light pulses. For greater clarity, I will make two artificial and unrealistic changes. I will send red and green pulses into the detector, representing the light that goes into the horizontal and the vertical arm, respectively. In reality, there is no distinction, just light apportioned at the beamsplitter. Light running towards M1 will be offset a little to the left, light coming back from M1 to the right, for better clarity. Same goes for M2. This, too, is different in a real detector. That said, here come the light pulses: 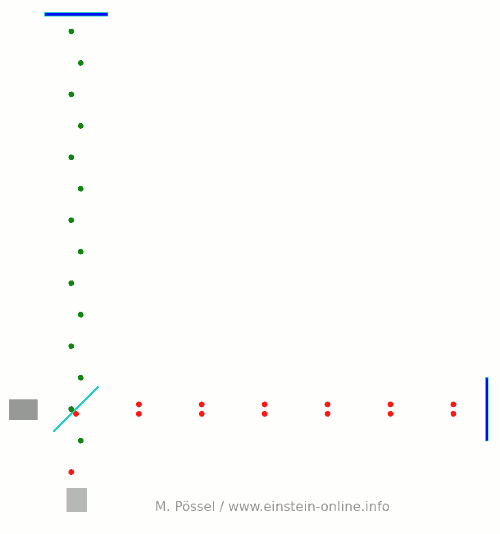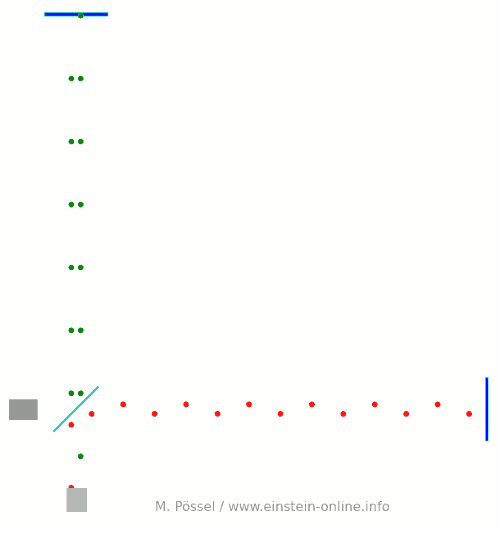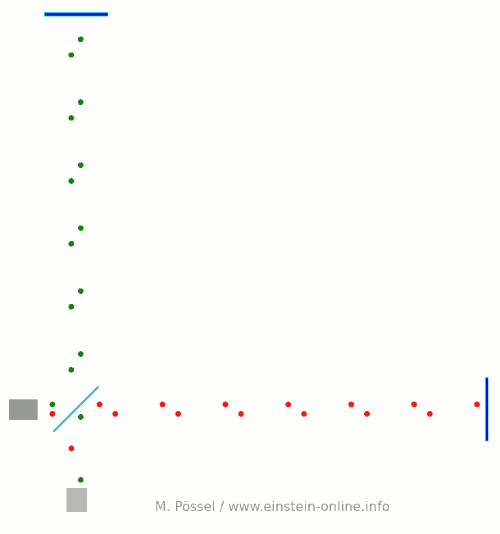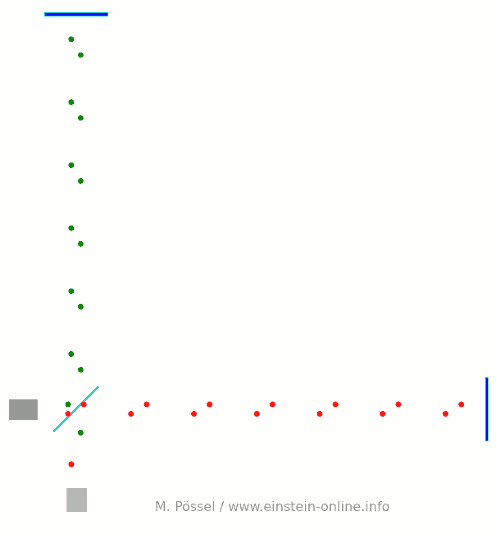Light starts at the light source to the left. Light that has left the source together, travels together (so green and red pulses are side by side) until the beam splitter. The beam splitter then sends the green pulses on their upward journey and lets the red pulses pass on their way towards the mirror on the right. All the particles that arrive back at the beamsplitter after reflection at M1 or M2. At the beamsplitter, they are directed towards the light detector at the bottom.

In this setup, the horizontal arm is slightly longer than the vertical arm. Red particles have to cover some extra distance. That is why they arrive at the detector a bit later, and we get an alternating rhythm: green, red, green, red, with equal distances in between. This will become important later on.

Here is a diagram, a kind of registration strip, which shows the arrival times for red and green pulses at the light detector (time is measured in “animation frames”): The pattern is clear: red and green pulses arrive evenly spaced, one after the other.

Bring on the gravitational wave!

Next, let’s switch on our standard gravitational wave (exaggerated, passing through the screen towards you, and so on). Here is the result: 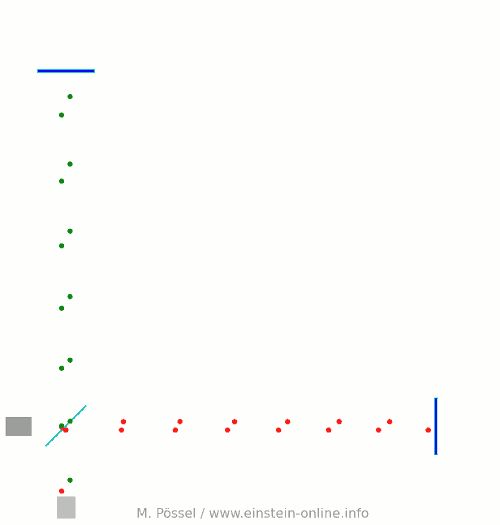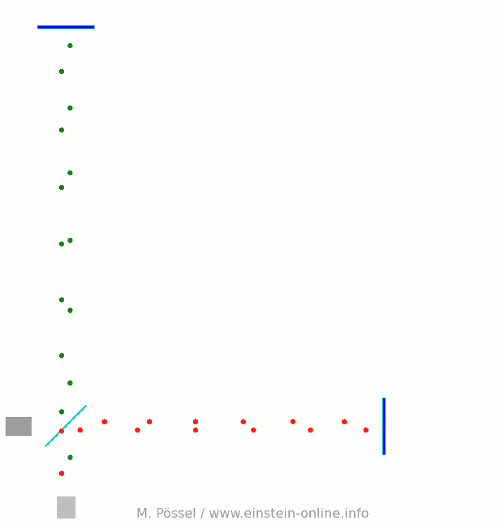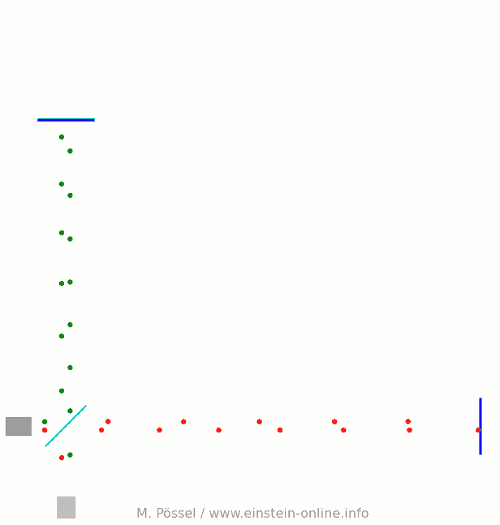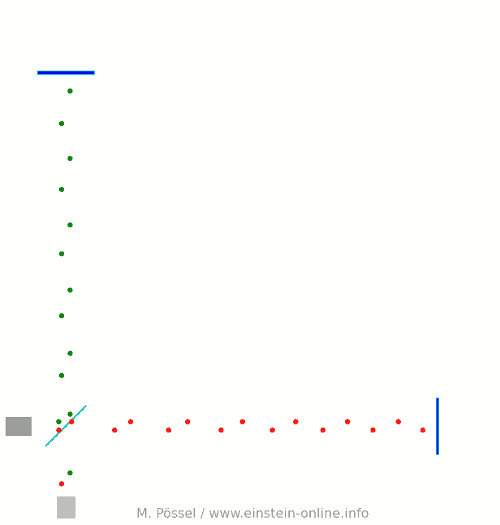We have trained our camera on the beamsplitter (so in our image, the beamsplitter doesn’t move). We ignore any slight changes in distance between beamsplitter and light source/light detector. Instead, we focus on the mirrors M1 and M2, which change their distance from the beamsplitter just as we would expect from the earlier animations.

Look at the way the pulses arrive at our light detector: sometimes red and green are almost evenly spaced, sometimes they close together. That is caused by the gravitational wave. Without the wave, we had strict regularity.

Here is the corresponding “registration strip” diagram. You can see that at some times, the light pulses of each color are closer together, at others, farther apart:

At the time I have marked with a hand-drawn arrow, red and green pulses arrive almost in unison!

The pattern is markedly different from the scenario without a gravitational wave. Detect this change in the pattern, and you have detected the gravitational wave.

Running interference

If you’ve wondered why detectors like LIGO are called interferometric gravitational wave detectors, we will need to think about waves a bit more. If not, let me just state that detectors like LIGO use the wave properties of light to measure the changes in pulse arrival rate you have seen in the last animation. To skip the details, feel free to jump ahead to the last section, “…and now for something a thousand times more complicated.”

Light is a wave, with crests and troughs corresponding to maxima and minima of the electric and of the magnetic field. While the animations I have shown you track the propagation of light pulses, they can also be used to understand what happens to a light wave in the interferometer. Just assume that each of the moving red and green dots in the detector marks the position of a wave crest.

Particles just add up. Take 2 particle and add 2 particles, and you will end up with 4 particles. But if you add up (combine, superimpose) waves, it depends. Sometimes, one wave plus another wave is indeed a bigger wave. Sometimes, it’s a smaller wave, or no wave at all. And sometimes it’s complicated.

When two waves are in perfect sync, the crests of the one aligning with the crests of the other, and the troughs aligning, too, you indeed get a bigger wave. The following diagram shows at which times the different parts of two light waves arrive at the light detector, and how they add up. (I’ve placed a dot on top of each crest; that is what the dots where meant to signify, after all.) 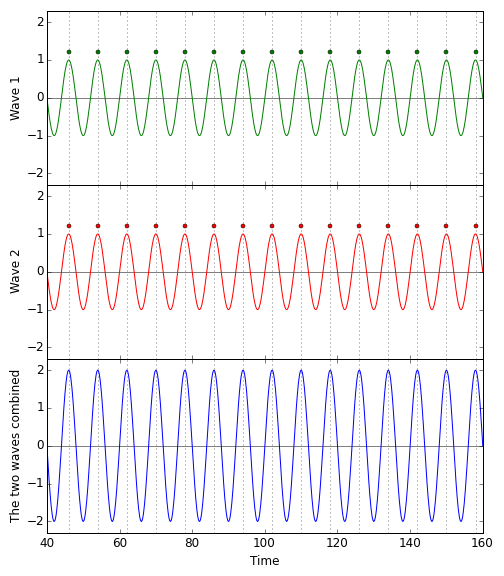On top, the green wave, perfectly aligned with the red wave (which, for clarity, is shown directly below the green wave). Add the two waves up, and you will get the (markedly stronger) blue wave in the bottom panel.

Not so if the two waves are maximally misaligned, the crests of each aligned with the troughs of the other. A crest and a trough cancel each other out. The sum of a wave and a maximally misaligned wave of equal strength is: no wave at all. Here is the corresponding diagram: 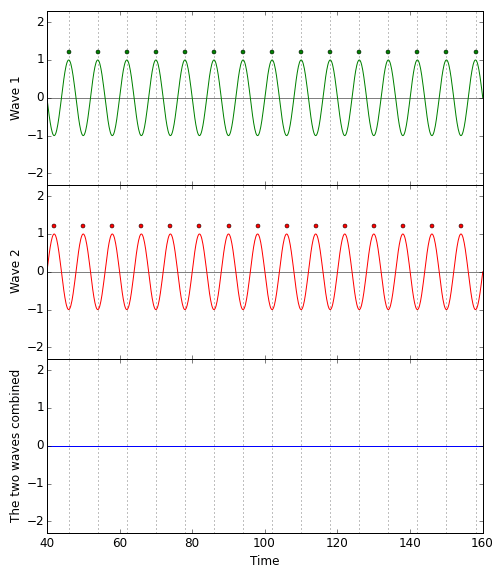Recall that this was exactly the setup for our gravitational wave detector in the absence of gravitational waves: Red and green pulses with equal spacing; troughs of the one wave perfectly aligned with the crests of the other. The result: No light at the light detector. (For realistic gravitational wave detectors, that is almost true.)

When a gravitational wave passes through the detector, the situation changes. Here is the corresponding pattern of pulse/wave crest arrival times for the animation above: 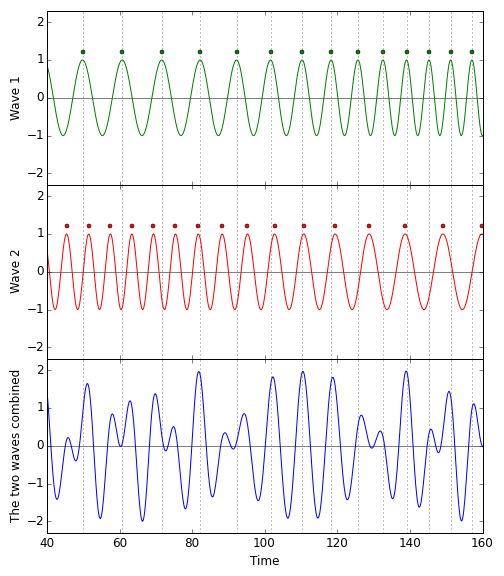The blue pattern, which is the sum of the red and the green, is complex. But it is not a flat line. There is light at the light detector where there was no light before, and the cause of the change is the gravitational wave passing through.

All in all, this makes a (highly simplified) version of how gravitational wave detectors such as LIGO work. Whatever the scientists will report this Thursday, it is based on light signals at the exit of such an interferometric detector.

And now for something a thousand times more complicated

Real gravitational wave detectors are, of course, much more complicated than that. I haven’t even started talking about the many disturbances scientists need to take into account – and to suppress as far as possible. How do you suspend the mirrors so that (at least for certain gravitational waves) they will indeed be influenced as if they were freely floating particles? How do you prevent seismic noise, cars or trains in the wider neighborhood and so on from moving your mirrors a tiny little bit (either by vibrations or by their own gravity)? What about fluctuations of the laser light?

Gravitational wave hunting is largely a hunt for noise, and for ways of suppressing that noise. The LIGO gravitational wave detectors and their kin are highly complex machines, with hundreds of control circuits, highly elaborate mirror suspensions, the most stable lasers known to physics (and some of the most high-powered). The technology has been contributed by numerous group from all over the world.

But all this is taking us too far, and I refer you to the pages of the detectors and collaborations for additional information:

LIGO pages at Caltech

Pages of the LIGO Scientific Collaboration

GEO 600 pages

VIRGO / EGO pages

You can find some further information about gravitational waves on the Einstein Online website:

Einstein Online: Spotlights on gravitational waves

Update: Gravitational Waves Discovered

February 8, 2016February 11, 2016 by Markus Pössel

Gravitational Waves and How They Distort Space

Gravitational waves distort space in a rhythmic fashion. These simple animations show how. — That's not a space worm. It's what a gravitational wave does to space according to Einstein's theory of general relativity.

It’s official: on February 11, 10:30 EST, there will be a big press conference about gravitational waves by the people running the gravitational wave detector LIGO. It’s a fair bet that they will announce the first direct detection of gravitational waves, predicted by Albert Einstein 100 years ago. If all goes as the scientists hope, this will be the kick-off for an era of gravitational wave astronomy: for learning about some of the most extreme and violent events in the cosmos by measuring the tiny ripples of space distortions that emanate from them.

Time to brush up on your gravitational wave knowledge, if you haven’t already done so! Here’s a visualization to help you – and we’ll go step by step to see what it means:

Einstein’s distorted spacetime

In the words of the eminent relativist John Wheeler, Einstein’s theory of general relativity can be summarized in two statements: Matter tells space and time how to curve. And (curved) space and time tell matter how to move. (Here is a slightly longer version on Einstein Online.)

Einstein published the final form of his theory in November 1915. By spring 1916, he had realized another consequence of distorting space and time: general relativity allows for gravitational waves, rhythmic distortions which propagate through space at the speed of light.

For quite some time, physicists weren’t sure whether these gravitational waves were real or a mathematical artifact within Einstein’s theory. (For more about this controversy, see Daniel Kennefick’s book “Traveling at the Speed of Thought and this article.) But since the 1980s, there has been indirect evidence for these waves (which earned its discoverers a Nobel prize, no less, in 1993).

Gravitational waves are emitted by orbiting bodies and certain other accelerated masses. Right now, major international efforts are underway to detect gravitational waves directly. Once detection is possible, the scientists hope to use gravitational waves to “listen” to some of the most violent processes in the universe: merging black holes and/or neutron stars, or the core region of supernova explosions.

Just as regular astronomy uses light and other forms of electromagnetic radiation to learn about distant objects, gravitational wave astronomy will decipher the information contained within gravitational waves. And if you go by recent rumors, gravitational wave astronomy might already have kicked off in mid-September 2015.

What do gravitational waves do?

But what do gravitational waves do? For that, let us look at a simplified, entirely hypothetical situation. (The following are variations on images and animations originally published here on Einstein Online.) Consider particles drifting in space, far from any sources of gravity. Imagine that the particles (red) are arranged in a circle around a center (marked in black):

If a simple gravitational wave were to pass through this image, coming directly at the reader, distances between these particles would change rhythmically as follows:

Note the distinctive pattern: When the circle is stretched in the vertical direction, it is compressed in the horizontal direction, and vice versa. That’s typical for gravitational waves (“quadrupole distortion”).

It’s important to keep in mind that this animation, and the ones that will follow, exaggerate the gravitational wave’s effect quite considerably. The gravitational waves detectors such as aLIGO hope to measure are much, much weaker. If our hypothetical circle of particles were as large as the Earth’s orbit around the Sun, a realistic gravitational wave would distort it by less than the diameter of a hydrogen atom.

Gravitational waves moving through space

The animation above shows what could be called a “gravitational oscillation.” To see the whole wave, we need to consider the third dimension.

We talk about a wave when oscillations propagate through space. Consider a water wave: At each point of the surface, we have an oscillation, with the surface rising and falling rhythmically. But it’s only the fact that this oscillation propagates, and that we can see a crest moving over the surface, that makes this into a wave.

It’s the same with gravitational waves. To see that, we will look not at a single circle of freely floating particles, but at many such circles, stacked one behind the other, forming the surface of a cylinder:

In this image, it’s hard to see which points are in front and which in the back. Let us join each particle to its nearest neighbors with a blue line, and let us also fill out the area between those lines. That way, the geometry is much more obvious:

Just remember that neither the lines nor the whitish surface is physical. On the contrary, if we want the particles to be maximally susceptible to the effect of the gravitational wave, we should make sure they are truly floating freely, and certainly they shouldn’t be linked in any way!

Now, let us see what the same gravitational wave we saw before does to this assembly of particles. From this perspective, the wave is passing from the right-hand side in the back towards the left-hand side on the front: As you can see, the wave is propagating through space. For instance, the point where the vertical distances within the circle of particles is maximal is moving towards the observer. The wave nature can be seen even more clearly if we look at this cylinder directly from the side:

What the animations show is just one kind of simple gravitational wave (“linearly polarized”). Here is another kind (“circularly polarized”):

This, then, is what the gravitational wave hunters are looking for. Except that they do not have particles floating in free space. Instead, their detectors contain test masses (notably large mirrors) elaborately suspended here on Earth, with laser light to detect the minute distance changes caused by gravitational waves.

More realistic gravitational wave signals, which contain information about merging black holes or the bulk motion of matter inside a supernova explosion, are more complicated still. They combine many simple waves of different frequencies, and the strength of such waves (their amplitude) will change over time in a characteristic fashion.

In these animations, gravitational waves look a bit like wriggling space worms. But these space worms could become the astronomers’ best friends, carrying information about the cosmos that is hard or even impossible to obtain in any other way.

[Don’t miss the sequel: Gravitational wave detectors: how they work]

Update: Gravitational Waves Detected

February 1, 2016February 23, 2017 by Fraser Cain

What is the Higgs Boson?

What is this thing we keep hearing about – the Higgs Boson, and why is it important?

Continue reading “What is the Higgs Boson?”

January 13, 2016January 13, 2016 by Matt Williams

What Are The Uses Of Electromagnets?

The Large Hadron Collider at CERN. Credit: CERN/LHC

Electromagnetism is one of the fundamental forces of the universe, responsible for everything from electric and magnetic fields to light. Originally, scientists believed that magnetism and electricity were separate forces. But by the late 19th century, this view changed, as research demonstrated conclusively that positive and negative electrical charges were governed by one force (i.e. magnetism).

Since that time, scientists have sought to test and measure electromagnetic fields, and to recreate them. Towards this end, they created electromagnets, a device that uses electrical current to induce a magnetic field. And since their initial invention as a scientific instrument, electromagnets have gone on to become a regular feature of electronic devices and industrial processes.

Continue reading “What Are The Uses Of Electromagnets?”

December 15, 2015April 7, 2016 by Matt Williams

What Are The Parts Of An Atom?

A depiction of the atomic structure of the helium atom. Credit: Creative Commons

Since the beginning of time, human beings have sought to understand what the universe and everything within it is made up of. And while ancient magi and philosophers conceived of a world composed of four or five elements – earth, air, water, fire (and metal, or consciousness) – by classical antiquity, philosophers began to theorize that all matter was actually made up of tiny, invisible, and indivisible atoms.

Since that time, scientists have engaged in a process of ongoing discovery with the atom, hoping to discover its true nature and makeup. By the 20th century, our understanding became refined to the point that we were able to construct an accurate model of it. And within the past decade, our understanding has advanced even further, to the point that we have come to confirm the existence of almost all of its theorized parts.

Continue reading “What Are The Parts Of An Atom?”

November 16, 2015December 23, 2015 by Vanessa Janek

Cosmologist Thinks a Strange Signal May Be Evidence of a Parallel Universe

A simulation of galaxies during the era of deionization in the early Universe. Credit: M. Alvarez, R. Kaehler, and T. AbelCredit: M. Alvarez, R. Kaehler, and T. Abel

In the beginning, there was chaos.

Hot, dense, and packed with energetic particles, the early Universe was a turbulent, bustling place. It wasn’t until about 300,000 years after the Big Bang that the nascent cosmic soup had cooled enough for atoms to form and light to travel freely. This landmark event, known as recombination, gave rise to the famous cosmic microwave background (CMB), a signature glow that pervades the entire sky.

Now, a new analysis of this glow suggests the presence of a pronounced bruise in the background — evidence that, sometime around recombination, a parallel universe may have bumped into our own.

Although they are often the stuff of science fiction, parallel universes play a large part in our understanding of the cosmos. According to the theory of eternal inflation, bubble universes apart from our own are theorized to be constantly forming, driven by the energy inherent to space itself.

Like soap bubbles, bubble universes that grow too close to one another can and do stick together, if only for a moment. Such temporary mergers could make it possible for one universe to deposit some of its material into the other, leaving a kind of fingerprint at the point of collision.

Ranga-Ram Chary, a cosmologist at the California Institute of Technology, believes that the CMB is the perfect place to look for such a fingerprint.

This image, the best map ever of the Universe, shows the oldest light in the universe. This glow, left over from the beginning of the cosmos called the cosmic microwave background, shows tiny changes in temperature represented by color. Credit: ESA and the Planck Collaboration. — The cosmic microwave background (CMB), a pervasive glow made of light from the Universe’s infancy, as seen by the Planck satellite in 2013. Tiny deviations in average temperature are represented by color. Credit: ESA and the Planck Collaboration.

After careful analysis of the spectrum of the CMB, Chary found a signal that was about 4500x brighter than it should have been, based on the number of protons and electrons scientists believe existed in the very early Universe. Indeed, this particular signal — an emission line that arose from the formation of atoms during the era of recombination — is more consistent with a Universe whose ratio of matter particles to photons is about 65x greater than our own.

There is a 30% chance that this mysterious signal is just noise, and not really a signal at all; however, it is also possible that it is real, and exists because a parallel universe dumped some of its matter particles into our own Universe.

After all, if additional protons and electrons had been added to our Universe during recombination, more atoms would have formed. More photons would have been emitted during their formation. And the signature line that arose from all of these emissions would be greatly enhanced.

Chary himself is wisely skeptical.

“Unusual claims like evidence for alternate Universes require a very high burden of proof,” he writes.

Indeed, the signature that Chary has isolated may instead be a consequence of incoming light from distant galaxies, or even from clouds of dust surrounding our own galaxy.

SO is this just another case of BICEP2? Only time and further analysis will tell.

Chary has submitted his paper to the Astrophysical Journal. A preprint of the work is available here.

October 13, 2015December 23, 2015 by Vanessa Janek

Shape-shifting neutrinos earn physicists the 2015 Nobel

Super-Kamiokande, a neutrino detector in Japan, holds 50,000 tons of ultrapure water surrounded by light tubes. Credit: Super-Kamiokande Observatory

What do Albert Einstein, Neils Bohr, Paul Dirac, and Marie Curie have in common? They each won the Nobel prize in physics. And today, Takaaki Kajita and Arthur McDonald have joined their ranks, thanks to a pioneering turn-of-the-century discovery: in defiance of long-held predictions, neutrinos shape-shift between multiple identities, and therefore must have mass.

The neutrino, a slight whiff of a particle that is cast off in certain types of radioactive decay, nuclear reactions, and high-energy cosmic events, could be called… shy. Electrically neutral but enormously abundant, half the time a neutrino could pass through a lightyear of lead without interacting with a single other particle. According to the Standard Model of particle physics, it has a whopping mass of zero.

As you can imagine, neutrinos are notoriously difficult to detect.

But in 1956, scientists did exactly that. And just a few years later, a trio of physicists determined that neutrinos came in not just one, not two, but three different types, or flavors: the electron neutrino, the muon neutrino, and the tau neutrino.

The first annotated neutrino event. Image credit: — The neutrino was first detected in 1956 by Clyde Cowan and Frederick Reines. In 1970, scientists captured the first image of a neutrino track in a hydrogen bubble chamber. *Image: Argonne National Laboratory*

But there was a problem. Sure, scientists had figured out how to detect neutrinos—but they weren’t detecting enough of them. In fact, the number of electron neutrinos arriving on Earth due to nuclear reactions in the Sun’s core was only one-third to one-half the number their calculations had predicted. What, scientists wondered, was happening to the rest?

Kajita, working at the Super-Kamiokande detector in Japan in 1998, and McDonald, working at the Sudbury Neutrino Observatory in Canada in 1999, determined that the electron neutrinos were not disappearing at all; rather, these particles were changing identity, spontaneously oscillating between the three flavor-types as they traveled through space.

Moreover, the researchers proclaimed, in order for neutrinos to make such transformations, they must have mass.

This is due to some quantum funny business having to do with the oscillations themselves. Grossly simplified, a massless particle, which always travels at the speed of light, does not experience time—Einstein’s theory of special relativity says so. But change takes time. Any particle that oscillates between identities needs to experience time in order for its state to evolve from one flavor to the the next.

The interior structure of the Sun. Credit: Wikipedia Commons/kelvinsong — Neutrinos are produced in abundance during fusion reactions at the center of our Sun, and oscillate between three different types, or *flavors*, on their way to Earth. *Image: Wikipedia Commons/kelvinsong*

Kajita and McDonald’s work showed that neutrinos must have a mass, albeit a very small one. But neutrinos are abundant in the Universe, and even a small mass has a large effect on all sorts of cosmic phenomena, from solar nuclear physics, where neutrinos are produced en masse, to the large-scale evolution of the cosmos, where neutrinos are ubiquitous.

The neutrino, no longer massless, is now considered to play a much larger role in these processes than scientists had originally believed.

What is more, the very existence of a massive neutrino undermines the theoretical basis of the Standard Model. In fact, Kajita’s and McDonald’s discovery provided some of the first evidence that the Standard Model might not be as airtight as had been previously believed, nudging scientists ever more in the direction of so-called “new physics.”

This is not the first time physicists have been awarded a Nobel prize for research into the nature of neutrinos. In 1988, Leon Lederman, Melvin Schwartz, and Jack Steinberger were awarded the prize for their discovery that neutrinos come in three flavors; in 1995, Frederick Reines won a Nobel for his detection of the neutrino along with Clyde Cowan; and in 2002, a Nobel was awarded to Raymond David Jr., the oldest person ever to receive a the prize in physics, and Masatoshi Koshiba for their detection of cosmic neutrinos.

Kajita, of the University of Tokyo, and McDonald, of Queen’s University in Canada, were awarded the prestigious prize this morning at a news conference in Stockholm.

August 12, 2015December 23, 2015 by Vanessa Janek

The Journey of Light, From the Stars to Your Eyes

The Milky Way from Earth. Image Credit: Kerry-Ann Lecky Hepburn (Weather and Sky Photography)

This week, millions of people will turn their eyes to the skies in anticipation of the 2015 Perseid meteor shower. But what happens on less eventful nights, when we find ourselves gazing upward simply to admire the deep, dark, star-spangled sky? Far away from the glow of civilization, we humans can survey thousands of tiny pinpricks of light. But how? Where does that light come from? How does it make its way to us? And how do our brains sort all that incoming energy into such a profoundly breathtaking sight?

Our story begins lightyears away, deep in the heart of a sun-like star, where gravity’s immense inward pressure keeps temperatures high and atoms disassembled. Free protons hurtle around the core, occasionally attaining the blistering energies necessary to overcome their electromagnetic repulsion, collide, and stick together in pairs of two.

Proton-proton fusion in a sun-like star. Credit: Borb

So-called diprotons are unstable and tend to disband as quickly as they arise. And if it weren’t for the subatomic antics of the weak nuclear force, this would be the end of the line: no fusion, no starlight, no us. However, on very rare occasions, a process called beta decay transforms one proton in the pair into a neutron. This new partnership forms what is known as deuterium, or heavy hydrogen, and opens the door to further nuclear fusion reactions.

Indeed, once deuterium enters the mix, particle pileups happen far more frequently. A free proton slams into deuterium, creating helium-3. Additional impacts build upon one another to forge helium-4 and heavier elements like oxygen and carbon.

Such collisions do more than just build up more massive atoms; in fact, every impact listed above releases an enormous amount of energy in the form of gamma rays. These high-energy photons streak outward, providing thermonuclear pressure that counterbalances the star’s gravity. Tens or even hundreds of thousands of years later, battered, bruised, and energetically squelched from fighting their way through a sun-sized blizzard of other particles, they emerge from the star’s surface as visible, ultraviolet, and infrared light.

Ta-da!

But this is only half the story. The light then has to stream across vast reaches of space in order to reach the Earth – a process that, provided the star of origin is in our own galaxy, can take anywhere from 4.2 years to many thousands of years! At least… from your perspective. Since photons are massless, they don’t experience any time at all! And even after eluding what, for any other massive entity in the Universe, would be downright interminable flight times, conditions still must align so that you can see even one twinkle of the light from a faraway star.

That is, it must be dark, and you must be looking up.

The incoming stream of photons then makes its way through your cornea and lens and onto your retina, a highly vascular layer of tissue that lines the back of the eye. There, each tiny packet of light impinges upon one of two types of photoreceptor cell: a rod, or a cone.

Most photons detected under the low-light conditions of stargazing will activate rod cells. These cells are so light-sensitive that, in dark enough conditions, they can be excited by a single photon! Rods cannot detect color, but are far more abundant than cones and are found all across the retina, including around the periphery.

The less numerous, more color-hungry cone cells are densely concentrated at the center of the retina, in a region called the fovea (this explains why dim stars that are visible in your side vision suddenly seem to disappear when you attempt to look at them straight-on). Despite their relative insensitivity, cone cells can be activated by very bright starlight, enabling you to perceive stars like Vega as blue and Betelgeuse as red.

But whether bright light or dim, every photon has the same endpoint once it reaches one of your eyes’ photoreceptors: a molecule of vitamin A, which is bound together with a specialized protein called an opsin. Vitamin A absorbs the light and triggers a signal cascade: ion channels open and charged particles rush across a membrane, generating an electrical impulse that travels up the optic nerve and into the brain. By the time this signal reaches your brain’s visual cortex, various neural pathways are already hard at work translating this complex biochemistry into what you once thought was a simple, intuitive, and poetic understanding of the heavens above…

The stars, they shine.

So the next time you go outside in the darker hours, take a moment to appreciate the great lengths it takes for just a single twinkle of light to travel from a series of nuclear reactions in the bustling center of a distant star, across the vastness of space and time, through your body’s electrochemical pathways, and into your conscious mind.

It gives every last one of those corny love songs new meaning, doesn’t it?

August 3, 2015December 23, 2015 by Bob King

The Resplendent Inflexibility of the Rainbow

A colorful piece of rainbow begs the question - why Roy G. Biv? Credit: Bob King

Children often ask simple questions that make you wonder if you really understand your subject. An young acquaintance of mine named Collin wondered why the colors of the rainbow were always in the same order — red, orange, yellow, green, blue, indigo, violet. Why don’t they get mixed up?

The familiar sequence is captured in the famous Roy G. Biv acronym, which describes the sequence of rainbow colors beginning with red, which has the longest wavelength, and ending in violet, the shortest. Wavelength — the distance between two successive wave crests — and frequency, the number of waves of light that pass a given point every second, determine the color of light.

The familiar colors of the rainbow spectrum with wavelengths shown in nanometers. Credit: NASA

The cone cells in our retinas respond to wavelengths of light between 650 nanometers (red) to 400 (violet). A nanometer is equal to one-billionth of a meter. Considering that a human hair is 80,000-100,000 nanometers wide, visible light waves are tiny things indeed.

So why Roy G. Biv and not Rob G. Ivy? When light passes through a vacuum it does so in a straight line without deviation at its top speed of 186,000 miles a second (300,000 km/sec). At this speed, the fastest known in the universe as described in Einstein’s Special Theory of Relativity, light traveling from the computer screen to your eyes takes only about 1/1,000,000,000 of second. Damn fast.

But when we look beyond the screen to the big, wide universe, light seems to slow to a crawl, taking all of 4.4 hours just to reach Pluto and 25,000 years to fly by the black hole at the center of the Milky Way galaxy. Isn’t there something faster? Einstein would answer with an emphatic “No!”

A laser beam (left) shining through a glass of water demonstrates how many times light changes speed — from 186,222 miles per second (mps) in air to 124,275 mps through the glass. It speeds up again to 140,430 mps in water, slows down when passing through the other side of the glass and then speeds up again when leaving the glass for the air. Credit: Bob King

One of light’s most interesting properties is that it changes speed depending on the medium through which it travels. While a beam’s velocity through the air is nearly the same as in a vacuum, “thicker” mediums slow it down considerably. One of the most familiar is water. When light crosses from air into water, say a raindrop, its speed drops to 140,430 miles a second (226,000 km/sec). Glass retards light rays to 124,275 miles/second, while the carbon atoms that make up diamond crunch its speed down to just 77,670 miles/second.

Why light slows down is a bit complicated but so interesting, let’s take a moment to describe the process. Light entering water immediately gets absorbed by atoms of oxygen and hydrogen, causing their electrons to vibrate momentarily before it’s re-emitting as light. Free again, the beam now travels on until it slams into more atoms, gets their electrons vibrating and gets reemitted again. And again. And again.

A ray of light refracted by a plastic block. Notice that the light bends twice - once when it enters (moving from air to plastic) and again when it exits (plastic to air). — A ray of light refracted by a plastic block. Notice that the light bends twice – once when it enters (moving from air to plastic) and again when it exits (plastic to air). The beam slows down on entering and then speeds up again when it exits.

Like an assembly line, the cycle of absorption and reemission continues until the ray exits the drop. Even though every photon (or wave – your choice) of light travels at the vacuum speed of light in the voids between atoms, the minute time delays during the absorption and reemission process add up to cause the net speed of the light beam to slow down. When it finally leaves the drop, it resumes its normal speed through the airy air.

Light rays get bent or refracted when they move from one medium to another. We've all seen the "broken pencil" effect when light travels from air into water. — Light rays get bent or refracted when they move from one medium to another. We’ve all seen the “broken pencil” effect when light travels from air into water.

Let’s return now to rainbows. When light passes from one medium to another and its speed drops, it also gets bent or refracted. Plop a pencil in a glass half filled with water and and you’ll see what I mean.

Up to this point, we’ve been talking about white light only, but as we all learned in elementary science, Sir Isaac Newton conducted experiments with prisms in the late 1600s and discovered that white light is comprised of all the colors of the rainbow. It’s no surprise that each of those colors travels at a slightly different speed through a water droplet. Red light interacts only weakly with the electrons of the atoms and is refracted and slowed the least. Shorter wavelength violet light interacts more strongly with the electrons and suffers a greater degree of refraction and slowdown.

Isaac Newton used a prism to separate light into its familiar array of colors. Like a prism, a raindrop refracts incoming sunlight, spreading it into an arc of rainbow colors with a radius of 42. Left: NASA image, right, public domain with annotations by the author — Isaac Newton used a prism to separate light into its familiar array of colors. Like a prism, a raindrop refracts incoming sunlight, spreading it into an arc of rainbow colors with a radius of 42. The colors spread out when light enter the drop and then spread out more when they leave and speed up. Left: NASA image, right, public domain with annotations by the author

Rainbows form when billions of water droplets act like miniature prisms and refract sunlight. Violet (the most refracted) shows up at the bottom or inner edge of the arc. Orange and yellow are refracted a bit less than violet and take up the middle of the rainbow. Red light, least affected by refraction, appears along the arc’s outer edge.

Rainbows are often double. The secondary bow results from light reflecting a second time inside the raindrop. When it emerges, the colors are reversed (red on the bottom instead of top), but the order of colors is preserved. Credit: Bob King

Because their speeds through water (and other media) are a set property of light, and since speed determines how much each is bent as they cross from air to water, they always fall in line as Roy G. Biv. Or the reverse order if the light beam reflects twice inside the raindrop before exiting, but the relation of color to color is always preserved. Nature doesn’t and can’t randomly mix up the scheme. As Scotty from Star Trek would say: “You can’t change the laws of physics!”

So to answer Collin’s original question, the colors of light always stay in the same order because each travels at a different speed when refracted at an angle through a raindrop or prism.

Light of different colors have both different wavelengths (distance between successive wave crests) and frequencies. In this diagram, red light has a longer wavelength and more "stretched out" waves compared to purple light of higher frequency. Credit: NASA — Light of different colors have both different wavelengths (distance between successive wave crests) and frequencies. In this diagram, red light has a longer wavelength and more “stretched out” waves compared to purple light of higher frequency. Credit: NASA

Not only does light change its speed when it enters a new medium, its wavelength changes, but its frequency remains the same. While wavelength may be a useful way to describe the colors of light in a single medium (air, for instance), it doesn’t work when light transitions from one medium to another. For that we rely on its frequency or how many waves of colored light pass a set point per second.

Higher frequency violet light crams in 790 trillion waves per second (cycles per second) vs. 390 trillion for red. Interestingly, the higher the frequency, the more energy a particular flavor of light carries, one reason why UV will give you a sunburn and red light won’t.

When a ray of sunlight enters a raindrop, the distance between each successive crest of the light wave decreases, shortening the beam’s wavelength. That might make you think that that its color must get “bluer” as it passes through a raindrop. It doesn’t because the frequency remains the same.

We measure frequency by dividing the number of wave crests passing a point per unit time. The extra time light takes to travel through the drop neatly cancels the shortening of wavelength caused by the ray’s drop in speed, preserving the beam’s frequency and thus color. Click HERE for a further explanation.

Why prisms/raindrops bend and separate light

Before we wrap up, there remains an unanswered question tickling in the back of our minds. Why does light bend in the first place when it shines through water or glass? Why not just go straight through? Well, light does pass straight through if it’s perpendicular to the medium. Only if it arrives at an angle from the side will it get bent. It’s similar to watching an incoming ocean wave bend around a cliff. For a nice visual explanation, I recommend the excellent, short video above.

Oh, and Collin, thanks for that question buddy!

July 23, 2015December 23, 2015 by Vanessa Janek

What’s the Big Deal About the Pentaquark?

The pentaquark, a novel arrangement of five elementary particles, has been detected at the Large Hadron Collider. This particle may hold the key to a better understanding of the Universe's strong nuclear force. [Image credit: CERN/LHCb experiment]

“Three quarks for Muster Mark!,” wrote James Joyce in his labyrinthine fable, Finnegan’s Wake. By now, you may have heard this quote – the short, nonsensical sentence that eventually gave the name “quark” to the Universe’s (as-yet-unsurpassed) most fundamental building blocks. Today’s physicists believe that they understand the basics of how quarks combine; three join up to form baryons (everyday particles like the proton and neutron), while two – a quark and an antiquark – stick together to form more exotic, less stable varieties called mesons. Rare four-quark partnerships are called tetraquarks. And five quarks bound in a delicate dance? Naturally, that would be a pentaquark. And the pentaquark, until recently a mere figment of physics lore, has now been detected at the LHC!

So what’s the big deal? Far from just being a fun word to say five-times-fast, the pentaquark may unlock vital new information about the strong nuclear force. These revelations could ultimately change the way we think about our superbly dense friend, the neutron star – and, indeed, the nature of familiar matter itself.

Physicists know of six types of quarks, which are ordered by weight. The lightest of the six are the up and down quarks, which make up the most familiar everyday baryons (two ups and a down in the proton, and two downs and an up in the neutron). The next heaviest are the charm and strange quarks, followed by the top and bottom quarks. And why stop there? In addition, each of the six quarks has a corresponding anti-particle, or antiquark.

Six types of quark, arranged from left to right by way of their mass, depicted along with the other elementary particles of the Standard Model. The Higgs boson was added to the right side of the menagerie in 2012. (Image Credit: Fermilab)

An important attribute of both quarks and their anti-particle counterparts is something called “color.” Of course, quarks do not have color in the same way that you might call an apple “red” or the ocean “blue”; rather, this property is a metaphorical way of communicating one of the essential laws of subatomic physics – that quark-containing particles (called hadrons) always carry a neutral color charge.

For instance, the three components of a proton must include one red quark, one green quark, and one blue quark. These three “colors” add up to a neutral particle in the same way that red, green, and blue light combine to create a white glow. Similar laws are in place for the quark and antiquark that make up a meson: their respective colors must be exactly opposite. A red quark will only combine with an anti-red (or cyan) antiquark, and so on.

The pentaquark, too, must have a neutral color charge. Imagine a proton and a meson (specifically, a type called a J/psi meson) bound together – a red, a blue, and a green quark in one corner, and a color-neutral quark-antiquark pair in the other – for a grand total of four quarks and one antiquark, all colors of which neatly cancel each other out.

Physicists are not sure whether the pentaquark is created by this type of segregated arrangement or whether all five quarks are bound together directly; either way, like all hadrons, the pentaquark is kept in check by that titan of fundamental dynamics, the strong nuclear force.

The strong nuclear force, as its name implies, is the unspeakably robust force that glues together the components of every atomic nucleus: protons and neutrons and, more crucially, their own constituent quarks. The strong force is so tenacious that “free quarks” have never been observed; they are all confined far too tightly within their parent baryons.

But there is one place in the Universe where quarks may exist in and of themselves, in a kind of meta-nuclear state: in an extraordinarily dense type of neutron star. In a typical neutron star, the gravitational pressure is so tremendous that protons and electrons cease to be. Their energies and charges melt together, leaving nothing but a snug mass of neutrons.

Physicists have conjectured that, at extreme densities, in the most compact of stars, adjacent neutrons within the core may even themselves disintegrate into a jumble of constituent parts.

The neutron star… would become a quark star.

The difference between a neutron star and a quark star (Chandra) — The difference between a neutron star and a quark star. (Image Credit: Chandra)

Scientists believe that understanding the physics of the pentaquark may shed light on the way the strong nuclear force operates under such extreme conditions – not only in such overly dense neutron stars, but perhaps even in the first fractions of a second following the Big Bang. Further analysis should also help physicists refine their understanding of the ways that quarks can and cannot combine.

The data that gave rise to this discovery – a whopping 9-sigma result! – came out of the LHC’s first run (2010-2013). With the supercollider now operating at double its original energy capacity, physicists should have no problem unraveling the mysteries of the pentaquark even further.

A preprint of the pentaquark discovery, which has been submitted to the journal Physical Review Letters, can be found here.