Posted on by Jean Tate

Stellar Parallax

Progress in astrometic accuracy (Credit: ESA)

[/caption]
Parallax is the apparent difference in the position (line of sight to) an object, when the object is viewed from different locations. So, when we observe that a star has apparently moved (not to be confused with it actually having moved – proper motion), when we look at it from two different locations on the Earth’s orbit around the Sun (i.e. on different dates), that’s stellar parallax! (And if the star does not seem to have moved? Well, its parallax is zero).

The furthest apart two locations on the Earth’s orbit can be is 2 au (two astronomical units), as when observations of an object are taken six months apart. By simple trigonometry (geometry), the distance to the object being observed is just the length of the baseline divided by the tangent of the parallax angle (the angular difference in the two lines of sight) … and since parallax angles are extremely small for stars (less than one arcsecond), the tangent of the angle is the same as the angle. This gives a natural unit of distance for stars, the parsec … which is the distance at which an object has a parallax of one arcsecond when viewed from a baseline of one au.

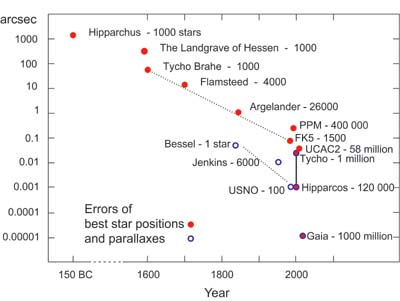
There was a pretty hot competition, among astronomers, to be the first to measure the parallax of a star (other than the Sun), back in the 1830s; the race was won by Friedrich Bessell (remember Bessell functions?), in 1838, with a measurement of the parallax of 61 Cygni (0.314 arcsecs, in case you were wondering; two other astronomers measured the parallax of different stars in the same year).

To date, the most accurate parallaxes (~1 milli-arcsec) are the 100,000 or so obtained by the ESA’s Hipparcos mission (which operated between 1989 and 1993; results published in 1997) … Hipparcos stands for High Precision Parallax Collecting Satellite, but is also a nod to the ancient Greek astronomer Hipparchus. The follow-up mission, Gaia (target launch date: 2012) will substantially improve on this (up to a billion stars, parallaxes as small as 20 micro-arcsec). Here’s a fun fact: Gaia will measure the gravitational deflection caused the Sun … across the whole sky (and detect that due to Mars, for stars near the line sight to it)!

Universe Today has several stories on, or featuring, stellar parallax; here are a few: New Stellar Neighbors Found, Chasing an Occultation, and Happy Birthday Johannes Kepler.

Distance in Space is an Astronomy Cast episode on this very topic!

References:
http://hyperphysics.phy-astr.gsu.edu/hbase/astro/para.html
http://starchild.gsfc.nasa.gov/docs/StarChild/questions/parallax.html

Posted on by Jean Tate

Megaparsec

velocity vs distance, from Hubble's 1929 paper

[/caption]
A megaparsec is a million parsecs (mega- is a prefix meaning million; think of megabyte, or megapixel), and as there are about 3.3 light-years to a parsec, a megaparsec is rather a long way. The standard abbreviation is Mpc.

Why do astronomers need to have such a large unit? When discussing distances like the size of a galaxy cluster, or a supercluster, or a void, the megaparsec is handy … just as it’s handy to use the astronomical unit (au) for solar system distances (for single galaxies, 1,000 parsecs – a kiloparsec, kpc – is a more natural scale; for cosmological distances, a gigaparsec (Gpc) is sometimes used).

Reminder: a parsec (a parallax of one arc-second, or arcsec) is a natural distance unit (for astronomers at least) because the astronomical unit (the length of the semi-major axis of the Earth’s orbit around the Sun, sorta) and arcsec are everyday units (again, for astronomers at least). Fun fact: even though the first stellar parallax distance was published in 1838, it wasn’t until 1913 that the word ‘parsec’ appeared in print!

As a parsec is approximately 3.09 x 1016 meters, a megaparsec is about 3.09 x 1022 meters.

You’ll most likely come across megaparsec first, and most often, in regard to the Hubble constant, which is the value of the slope of the straight line in a graph of the Hubble relationship (or Hubble’s Law) – redshift vs distance. As redshift is in units of kilometers per second (km/s), and as distance is in units of megaparsecs (for the sorts of distances used in the Hubble relationship), the Hubble constant is nearly always stated in units of km/s/Mpc (e.g. 72 +/- 8 km/s/Mpc, or 72 +/- 8 km s-1 Mpc-1 – that’s its estimated value from the Hubble Key Project).

John Huchra’s page on the Hubble constant is great for seeing megaparsecs in action.

Given the ubiquity of megaparsecs in extragalactic astronomy, hardly any Universe Today article on this topic is without its mention! Some examples: Chandra Confirms the Hubble Constant, Radio Astronomy Will Get a Boost With the Square Kilometer Array, and Astronomers Find New Way to Measure Cosmic Distances.

Questions Show #7, an Astronomy Cast episode, has megaparsecs in action, as does this other Questions Show.

Posted on by John Carl Villanueva

How Long is a Light Year?

This visible-light image shows the galaxy dubbed UGC 3789, which is 160 million light-years from Earth. Credit: STScI

A light year is the distance light can travel in vacuum in one year’s time. This distance is equivalent to roughly 9,461,000,000,000 km or 5,878,000,000,000 miles. This is such a large distance. For comparison, consider the circumference of the Earth when measured at the equator: 40,075 km.

You can even throw in the center to center distance between the Earth and the Moon, 384,403 km, and that value would still pale in comparison to 1 light year. Pluto, at its farthest orbit distance from the Sun, is only about 7,400,000,000 km from the center of our Solar System.

Because of its great scale, the light year is one of the units of distance used for astronomical objects. For example, Andromeda Galaxy, which is the nearest spiral galaxy from the Milky Way, is approximately 2.5 million light years away. Alpha Centauri, the nearest star system from our own Solar System is only 4.37 light years away.

Imagine using miles or kilometers when describing the diameter of the Milky Way Galaxy, some 100,000 light years. Expressed in km or mi in expanded notation, that could occupy a lot of space on this page. Just look at the first paragraph, wherein we described 1 light year, to see what I mean. Of course, one may argue that we can still use scientific notation. But well, some people easily get daunted by the mere sight of exponents.

Although the light year has a more familiar ring to us, having perhaps heard about it quite often in sci-fi films or in magazines, it is not the most widely used unit of distance in astrometry, the branch of astronomy that deals with measurements and positions of celestial bodies. That assignment is given to the parsec. 1 parsec is approximately equal to 3.26 light years.

Another commonly used unit of distance is the astronomical unit or AU, wherein 1 AU is the average distance between the Earth and the Sun, and is roughly equivalent to 150,000,000 km. It is normally used when describing distances within the Milky Way.

Always remember that the ‘year’ we have been referring to here is not based in the internationally-accepted Gregorian Calendar. Instead, ‘year’ here refers to the Julian year. 1 Julian year is equivalent to 365.25 days or 31,557,600 seconds. The Julian calendar does not designate dates, hence is different from the Gregorian Calendar.

We have some related articles here in Universe Today. Here are the links:

Here are the links of two more articles from NASA:

Here are two episodes at Astronomy Cast that you might want to check out as well:

Source: NASA