Posted on by Nancy Atkinson

Gravity Probe B Confirms Two of Einstein’s Space-Time Theories

Einstein's predicted geodetic and frame-dragging effects, and the Schiff Equation for calculating them. Credit: Stanford University

[/caption]

Researchers have confirmed two predictions of Albert Einstein’s general theory of relativity, concluding one of NASA’s longest-running projects. The Gravity Probe B experiment used four ultra-precise gyroscopes housed in an Earth-orbiting satellite to measure two aspects of Einstein’s theory about gravity. The first is the geodetic effect, or the warping of space and time around a gravitational body. The second is frame-dragging, which is the amount a spinning object pulls space and time with it as it rotates.

Gravity Probe-B determined both effects with unprecedented precision by pointing at a single star, IM Pegasi, while in a polar orbit around Earth. If gravity did not affect space and time, GP-B’s gyroscopes would point in the same direction forever while in orbit. But in confirmation of Einstein’s theories, the gyroscopes experienced measurable, minute changes in the direction of their spin, while Earth’s gravity pulled at them.

The project as been in the works for 52 years.

The findings are online in the journal Physical Review Letters.

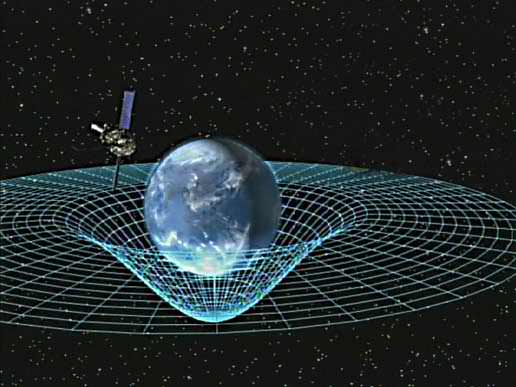
Artist concept of Gravity Probe B orbiting the Earth to measure space-time, a four-dimensional description of the universe including height, width, length, and time. Image credit: NASA

“Imagine the Earth as if it were immersed in honey,”.said Francis Everitt, Gravity Probe-B principal investigator at Stanford University. “As the planet rotates, the honey around it would swirl, and it’s the same with space and time,” “GP-B confirmed two of the most profound predictions of Einstein’s universe, having far-reaching implications across astrophysics research. Likewise, the decades of technological innovation behind the mission will have a lasting legacy on Earth and in space.”

NASA began development of this project starting in the fall of 1963 with initial funding to develop a relativity gyroscope experiment. Subsequent decades of development led to groundbreaking technologies to control environmental disturbances on spacecraft, such as aerodynamic drag, magnetic fields and thermal variations. The mission’s star tracker and gyroscopes were the most precise ever designed and produced.

GP-B completed its data collection operations and was decommissioned in December 2010.

“The mission results will have a long-term impact on the work of theoretical physicists,” said Bill Danchi, senior astrophysicist and program scientist at NASA Headquarters in Washington. “Every future challenge to Einstein’s theories of general relativity will have to seek more precise measurements than the remarkable work GP-B accomplished.”

Innovations enabled by GP-B have been used in GPS technologies that allow airplanes to land unaided. Additional GP-B technologies were applied to NASA’s Cosmic Background Explorer mission, which accurately determined the universe’s background radiation. That measurement is the underpinning of the big-bang theory, and led to the Nobel Prize for NASA physicist John Mather.

The drag-free satellite concept pioneered by GP-B made a number of Earth-observing satellites possible, including NASA’s Gravity Recovery and Climate Experiment and the European Space Agency’s Gravity field and steady-state Ocean Circulation Explorer. These satellites provide the most precise measurements of the shape of the Earth, critical for precise navigation on land and sea, and understanding the relationship between ocean circulation and climate patterns.

GP-B also advanced the frontiers of knowledge and provided a practical training ground for 100 doctoral students and 15 master’s degree candidates at universities across the United States. More than 350 undergraduates and more than four dozen high school students also worked on the project with leading scientists and aerospace engineers from industry and government. One undergraduate student who worked on GP-B became the first female astronaut in space, Sally Ride. Another was Eric Cornell who won the Nobel Prize in Physics in 2001.

“GP-B adds to the knowledge base on relativity in important ways and its positive impact will be felt in the careers of students whose educations were enriched by the project,” said Ed Weiler, associate administrator for the Science Mission Directorate at NASA Headquarters.

Sources: NASA, Stanford University

Posted on by Jean Tate

This is Getting Boring: General Relativity Passes Yet another Big Test!

Princeton University scientists (from left) Reinabelle Reyes, James Gunn and Rachel Mandelbaum led a team that analyzed more than 70,000 galaxies and demonstrated that the universe - at least up to a distance of 3.5 billion light years from Earth - plays by the rules set out by Einstein in his theory of general relativity. (Photo: Brian Wilson)

[/caption]
Published in 1915, Einstein’s theory of general relativity (GR) passed its first big test just a few years later, when the predicted gravitational deflection of light passing near the Sun was observed during the 1919 solar eclipse.

In 1960, GR passed its first big test in a lab, here on Earth; the Pound-Rebka experiment. And over the nine decades since its publication, GR has passed test after test after test, always with flying colors (check out this review for an excellent summary).

But the tests have always been within the solar system, or otherwise indirect.

Now a team led by Princeton University scientists has tested GR to see if it holds true at cosmic scales. And, after two years of analyzing astronomical data, the scientists have concluded that Einstein’s theory works as well in vast distances as in more local regions of space.

A partial map of the distribution of galaxies in the SDSS, going out to a distance of 7 billion light years. The amount of galaxy clustering that we observe today is a signature of how gravity acted over cosmic time, and allows as to test whether general relativity holds over these scales. (M. Blanton, SDSS)

The scientists’ analysis of more than 70,000 galaxies demonstrates that the universe – at least up to a distance of 3.5 billion light years from Earth – plays by the rules set out by Einstein in his famous theory. While GR has been accepted by the scientific community for over nine decades, until now no one had tested the theory so thoroughly and robustly at distances and scales that go way beyond the solar system.

Reinabelle Reyes, a Princeton graduate student in the Department of Astrophysical Sciences, along with co-authors Rachel Mandelbaum, an associate research scholar, and James Gunn, the Eugene Higgins Professor of Astronomy, outlined their assessment in the March 11 edition of Nature.

Other scientists collaborating on the paper include Tobias Baldauf, Lucas Lombriser and Robert Smith of the University of Zurich and Uros Seljak of the University of California-Berkeley.

The results are important, they said, because they shore up current theories explaining the shape and direction of the universe, including ideas about dark energy, and dispel some hints from other recent experiments that general relativity may be wrong.

“All of our ideas in astronomy are based on this really enormous extrapolation, so anything we can do to see whether this is right or not on these scales is just enormously important,” Gunn said. “It adds another brick to the foundation that underlies what we do.”

GR is one, of two, core theories underlying all of contemporary astrophysics and cosmology (the other is the Standard Model of particle physics, a quantum theory); it explains everything from black holes to the Big Bang.

In recent years, several alternatives to general relativity have been proposed. These modified theories of gravity depart from general relativity on large scales to circumvent the need for dark energy, dark matter, or both. But because these theories were designed to match the predictions of general relativity about the expansion history of the universe, a factor that is central to current cosmological work, it has become crucial to know which theory is correct, or at least represents reality as best as can be approximated.

“We knew we needed to look at the large-scale structure of the universe and the growth of smaller structures composing it over time to find out,” Reyes said. The team used data from the Sloan Digital Sky Survey (SDSS), a long-term, multi-institution telescope project mapping the sky to determine the position and brightness of several hundred million galaxies and quasars.

By calculating the clustering of these galaxies, which stretch nearly one-third of the way to the edge of the universe, and analyzing their velocities and distortion from intervening material – due to weak lensing, primarily by dark matter – the researchers have shown that Einstein’s theory explains the nearby universe better than alternative theories of gravity.

Some of the 70,000 luminous galaxies in SDSS analyzed (Image: SDSS Collaboration)

The Princeton scientists studied the effects of gravity on the SDSS galaxies and clusters of galaxies over long periods of time. They observed how this fundamental force drives galaxies to clump into larger collections of galaxies and how it shapes the expansion of the universe.

Critically, because relativity calls for the curvature of space to be equal to the curvature of time, the researchers could calculate whether light was influenced in equal amounts by both, as it should be if general relativity holds true.

“This is the first time this test was carried out at all, so it’s a proof of concept,” Mandelbaum said. “There are other astronomical surveys planned for the next few years. Now that we know this test works, we will be able to use it with better data that will be available soon to more tightly constrain the theory of gravity.”

Firming up the predictive powers of GR can help scientists better understand whether current models of the universe make sense, the scientists said.

“Any test we can do in building our confidence in applying these very beautiful theoretical things but which have not been tested on these scales is very important,” Gunn said. “It certainly helps when you are trying to do complicated things to understand fundamentals. And this is a very, very, very fundamental thing.”

“The nice thing about going to the cosmological scale is that we can test any full, alternative theory of gravity, because it should predict the things we observe,” said co-author Uros Seljak, a professor of physics and of astronomy at UC Berkeley and a faculty scientist at Lawrence Berkeley National Laboratory who is currently on leave at the Institute of Theoretical Physics at the University of Zurich. “Those alternative theories that do not require dark matter fail these tests.”

Sources: “Princeton scientists say Einstein’s theory applies beyond the solar system” (Princeton University), “Study validates general relativity on cosmic scale, existence of dark matter” (University of California Berkeley), “Confirmation of general relativity on large scales from weak lensing and galaxy velocities” (Nature, arXiv preprint)

Posted on by Jean Tate

Gravity Formula

The gravity formula that most people remember, or think of, is the equation which captures Newton’s law of universal gravitation, which says that the gravitational force between two objects is proportional to the mass of each, and inversely proportional to the distance between them. It is usually written like this (G is the gravitational constant):

F = Gm1m2/r2

Another, common, gravity formula is the one you learned in school: the acceleration due to the gravity of the Earth, on a test mass. This is, by convention, written as g, and is easily derived from the gravity formula above (M is the mass of the Earth, and r its radius):

g = GM/r2

In 1915, Einstein published his general theory of relativity, which not only solved a many-decades-long mystery concerning the observed motion of the planet Mercury (the mystery of why Uranus’ orbit did not match that predicted from applying Newton’s law was solved by the discovery of Neptune, but no hypothetical planet could explain why Mercury’s orbit didn’t), but also made a prediction that was tested just a few years’ later (deflection of light near the Sun). Einstein’s theory contains many gravity formulae, most of which are difficult to write down using only simple HTML scripts (so I’m not going to try).

The Earth is not a perfect sphere – the distance from surface to center is smaller at the poles than the equator, for example – and it is rotating (which means that the force on an object includes the centripetal acceleration due to this rotation). For people who need accurate formulae for gravity, both on the Earth’s surface and above it, there is a set of international gravity formulae which define what is called theoretical gravity, or normal gravity, g0. This corrects for the variation in g due to latitude (and so both the force due to the Earth’s rotation, and its non-spherical shape).

Here are some links that you can follow to learn more about gravity formulae (or gravity formulas): Newton’s theory of “Universal Gravitation” (NASA), International Gravity Formula(e) (University of Oklahoma), and Newton’s Law of Gravity (University of Oregon).

Many aspects of gravity, including a gravity formula or three, are covered in various Universe Today articles. For example, New Research Confirms Einstein, Milky Way Dwarf Galaxies Thwart Newtonian Gravity?, and Modifying Gravity to Account for Dark Matter. Here’s some information on 0 gravity.

Astronomy Cast’s episode Gravity gives you much more on not just one gravity formula, but several; and Gravitational Waves is good too. Be sure to check them out!

Sources:
University of Nebraska-Lincoln
NASA
UT-Knoxville

Posted on by Jean Tate

What is Space?

First, some simple answers: space is everything in the universe beyond the top of the Earth’s atmosphere – the Moon, where the GPS satellites orbit, Mars, other stars, the Milky Way, black holes, and distant quasars. Space also means what’s between planets, moons, stars, etc – it’s the near-vacuum otherwise known as the interplanetary medium, the interstellar medium, the inter-galactic medium, the intra-cluster medium, etc; in other words, it’s very low density gas or plasma (‘space physics’ is, in fact, just a branch of plasma physics!).

But you really want to know what space is, don’t you? You’re asking about the thing that’s like time, or mass.

And one simple, but profound, answer to the question “What is space?” is “that which you measure with a ruler”. And why is this a profound answer? Because thinking about it lead Einstein to develop first the theory of special relativity, and then the theory of general relativity. And those theories overthrew an idea that was built into physics since before the time of Newton (and built into philosophy too); namely, the idea of absolute space (and time). It turns out that space isn’t something absolute, something you could, in principle, measure with lots of rulers (and lots of time), and which everyone else who did the same thing would agree with you on.

Space, in the best theory of physics on this topic we have today – Einstein’s theory of general relativity (GR) – is a component of space-time, which can be described very well using the math in GR, but which is difficult to envision with our naïve intuitions. In other words, “What is space?” is a question I can’t really answer, in the short space I have in this Guide to Space article.

More reading: What is space? (ESA), What is space? (National Research Council of Canada), Ned Wright’s Cosmology Tutorial, and Sean Carroll’s Cosmology Primer pretty much cover this vast topic, from kids’ to physics undergrad’ level.

It’s hard to know just what Universe Today articles to recommend, because there are so many! Space Elevator? Build it on the Moon First illustrates one meaning of the word ‘space’; for meanings closer to what I’ve covered here, try New Way to Measure Curvature of Space Could Unite Gravity Theory, and Einstein’s General Relativity Tested Again, Much More Stringently.

Astronomy Cast episodes Einstein’s Theory of Special Relativity, Einstein’s Theory of General Relativity, Large Scale Structure of the Universe, and Coordinate Systems, are all good, covering as they do different ways to answer the question “What is space?”

Source: ESA

Posted on by Jean Tate

Gravity Equation

There is not one, not two, not even three gravity equations, but many!

The one most people know describes Newton’s universal law of gravitation:

F = Gm1m2/r2,
where F is the force due to gravity, between two masses (m1 and m2), which are a distance r apart; G is the gravitational constant.

From this is it straightforward to derive another, common, gravity equation, that which gives the acceleration due to gravity, g, here on the surface of the Earth:

g = GM/r2,
Where M is the mass of the Earth, r the radius of the Earth (or distance between the center of the Earth and you, standing on its surface), and G is the gravitational constant.

With its publication in the early years of the last century, Einstein’s theory of general relativity (GR) became a much more accurate theory of gravity (the theory has been tested extensively, and has passed all tests, with flying colors, to date). In GR, the gravity equation usually refers to Einstein’s field equations (EFE), which are not at all straight-forward to write, let alone explain (so I’m going to write them … but not explain them!):

G?? = 8?G/c4 T??

G (without the subscripts) is the gravitational constant, and c is the speed of light.

Finally, here’s a acceleration of gravity equation you’ve probably never heard of before:

a = ?(GMa0/r),

where a is the acceleration a star feels, due to gravity under MOND (MOdified Newtonian Dynamics), an alternative theory of gravity, M is the mass of a galaxy, r the distance between the star in the outskirts of that galaxy and its center, G the gravitational constant, and a0 a new constant.

Some websites which contain more on gravity equations, for your interest and enjoyment: Newton’s Theory of “Universal Gravitation” (NASA), Einstein’s equation of gravity (University of Wisconsin Madison – heavy), and Gravity Formula (University of Nebraska-Lincoln).

Universe Today, as you would expect, has several stories relevant to gravity equations; here are a few: See the Universe with Gravity Eyes, A Case of MOND Over Dark Matter, and Flyby Anomalies Explained?. Here’s an article about 0 gravity.

Gravity, an Astronomy Cast episode, has more on gravity equations, as do several Astronomy Cast Question Shows, such as September 26th, 2008, and March 31st, 2009.

Sources:
University of Nebraska-Lincoln
NASA
UT-Knoxville

Posted on by Jean Tate

Cosmological Constant

Seven Year Microwave Sky (Credit: NASA/WMAP Science Team)

[/caption]
The cosmological constant, symbol Λ (Greek capital lambda), was ‘invented’ by Einstein, not long after he published his theory of general relativity (GR). It appears on the left-hand side of the Einstein field equations.

Einstein added this term because he – along with all other astronomers and physicists of the time – thought the universe was static (the cosmological constant can make a universe filled with mass-energy static, neither expanding nor contracting). However, he very quickly realized that this wouldn’t work, because such a universe would be unstable … and quickly turn into one either expanding or contracting! Not long afterwards, Hubble (actually Vesto Slipher) discovered that the universe is, in fact, expanding, so the need for a cosmological constant went away.

Until 1998.

In that year, two teams of astronomers independently announced that distant Type Ia supernovae did not have the apparent luminosity they should, in a universe composed almost entirely of mass-energy in the form of baryons (ordinary matter) and cold dark matter.

Dark Energy had been discovered: dark energy is a form of mass-energy that has a constant density throughout the universe, and perhaps throughout time as well; counter-intuitively, it causes the expansion of the universe to accelerate (i.e. it acts kinda like anti-gravity). The most natural form of dark energy is the cosmological constant.

A great deal of research has gone into trying to discover if dark energy is, in fact, just the cosmological constant, or if it is quintessence, or something else. So far, results from observations of the CMB (by WMAP, mainly), of BAO (baryon acoustic oscillations, by extensive surveys of galaxies), and of high-redshift supernovae (by many teams) are consistent with dark energy being the cosmological constant.

So if the cosmological constant is (a) mass-energy (density), it can be expressed as kilograms (per cubic meter), can’t it? Yes, and the best estimate today is 7.3 x 10-27 kg m 3.

Ned Wright’s Cosmology Tutorial (UCLA) and Sean Carroll’s Cosmology Primer (California Institute of Technology) between them cover not only the cosmological constant, but also cosmology! NASA’s What Is A Cosmological Constant? is a great one-page intro.

Universe Today has many, many stories featuring the cosmological constant! Here are a few to whet your appetite: Universe to WMAP: LCDM Rules, OK?, Einstein’s Cosmological Constant Predicts Dark Energy, and No “Big Rip” in our Future: Chandra Provides Insights Into Dark Energy.

There are many Astronomy Cast episodes which include discussion of the cosmological constant … these are among the best: The Big Bang and Cosmic Microwave Background, The Important Numbers in the Universe, and the March 18th, 2009 Questions Show.

Sources:
http://map.gsfc.nasa.gov/universe/uni_accel.html
http://super.colorado.edu/~michaele/Lambda/lambda.html
http://en.wikipedia.org/wiki/Cosmological_constant